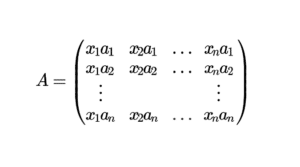Retrouve ici toutes les annales (et leurs moindres détails) de l’épreuve de mathématiques Ecricome en option maths approfondies depuis 2000. Ce tableau est un extrait du méga répertoire d’annales que tu peux télécharger en format Excel. N’hésite pas à consulter cet article pour avoir plus d’informations sur le système d’abréviations et des conseils sur la façon dont tu peux t’organiser avec ce tableau.
Ce répertoire est en constante amélioration. Si jamais tu souhaites contribuer à son évolution, n’hésite pas à nous suggérer toute remarque, toute erreur ou tout ajout (une notion hors programme non mentionnée, par exemple…) à ces deux adresses mail : sarah.trova@gmail.com et jean_sebastien.duprat@edu.escp.eu
Répertoire des annales de maths ECRICOME approfondies
Les corrections appartiennent à leurs auteurs respectifs
| Année/sujet | Correction | Type d’exo | Chapitres (analyse…) | Thème principal | Notions du programme utilisées | Notions hors programme utilisées | À quel moment le faire ? | Difficulté | Intérêt | Vision générale, notes personnelles | Rapport du jury | Résumé du rapport du jury |
| 2000 | correction | exercice 1 | ALGÈBRE BILI | étude des matrices de type \(n\) | matrices, diagonalisation, projecteurs orthogonaux | matrices de type \(n\) telles que \({}^tA=A^n\) | 2A | facile | ★★ | il existe des plus intéressants, si tu veux faire un exo, je te conseille le 1er | / | |
| exercice 2 | PROBAS, ANALYSE | étude d’un max de variables aléatoires | VA à densité, séries, probabilités conditionnelles | 2A | moyen | ★★★ méthodes classiques | ||||||
| problème | PROBAS | problème du statisticien | probas discrètes | 1A | moyen | ★ | ||||||
| 2001 | correction | exercice 1 | PROBAS | valeur absolue de la différence de deux lois exponentielles | variables à densité, produit de convolution | 2A | moyen | ★★★ méthodes classiques | exercices à faire plutôt indépendamment en fonction de tes besoins, de meilleurs exercices existent | / | ||
| exercice 2 | ALGÈBRE BILI | quelques calculs avec le produit scalaire canonique de \(\mathcal{M}_{n}(\mathbb{R})\) | produits scalaires, projections orthogonales | 2A | moyen | ★★ | ||||||
| problème | PROBAS | étude d’un jeu de hasard avec pile ou face | probabilités discrètes, stabilité d’un intervalle, suites, B-T | 2A | difficile | ★ | ||||||
| 2002 | correction | exercice 1 | COMPLEXES | exercices à faire plutôt indépendamment | / | |||||||
| exercice 2 | ANALYSE | étude d’une série | séries, intégrales | 1A | moyen | ★★★ méthodes classiques | ||||||
| problème | HORS PROGRAMME : ÉTUDE SUR OUVERTS | |||||||||||
| 2003 | correction | exercice 1 | ANALYSE | développement asymptotique d’une suite définie par \(u_{n+1} = u_n + u_n^2\) | suites numériques | 1A | moyen | ★ | à faire absolument, très complet | rapport 2003 | / | |
| exercice 2 | ALGÈBRE BILI | étude des matrices symétriques et antisymétriques | produits scalaires, matrices symétriques, Cauchy-Schwarz | 2A | moyen | ★★★ méthodes classiques | ||||||
| problème | TOUT | construction d’intervalles de confiance pour la variance de lois normales | variables à densité, intervalles de confiance, matrices symétriques, diagonalisation, estimateur | loi du khi-deux | 2A | difficile | ★★★ TB, à faire absolument pour t’entraîner aux intervalles de confiance | |||||
| 2004 | correction | exercice 1 | ALGÈBRE | matrices commutant avec une matrice de \(\mathcal{M}_{n}(\mathbb{R})\) possédant \(n\) VP | diagonalisation, polynômes de matrices | 1A | facile | ★ | méthodes peu classiques, mais qui restent intéressantes | rapport 2004 | / | |
| exercice 2 | ANALYSE | étude de la suite de terme général \(I_n=\displaystyle \int_{0}^{\frac{\pi}{4}} \frac{1}{\cos^n(x)}, \mathrm{d}t\) |
fonctions d’une variable, intégration sur un segment, suites | 1A | moyen | ★★ | ||||||
| problème | PROBAS | étude d’un jeu de hasard avec une urne | suites, probas discrètes, séries | 1A | difficile | ★★★ | ||||||
| 2005 | correction | exercice 1 | ALGÈBRE BILI | diagonalisation d’une matrice symétrique à paramètres | diagonalisation, matrices symétriques, fonctions trois variables | quotients de Rayleigh | 2A | moyen | ★★ | à faire absolument, TB pour réviser certaines notions précises | rapport 2005 | / |
| exercice 2 | ANALYSE | étude d’une suite récurrente | suites numériques | 1A | moyen | ★★★ TB pour t’entraîner aux suites | ||||||
| problème | PROBAS, ANALYSE | loi de Student, loi de Cauchy et lois normales | intégrales impropres, VA à densité, produit de convolution | loi de Student, loi de Cauchy | 2A | moyen | ★★★ méthodes classiques | |||||
| 2006 | correction | exercice 1 | ALGÈBRE BILI | réduction simultanée d’un ensemble d’endomorphismes de \(\mathbb R^3\) | espaces euclidiens, valeurs propres | 2A | moyen | ★ | à faire absolument, très complet | / | ||
| exercice 2 | ANALYSE | étude d’une fonction définie par une intégrale | intégrales impropres, fonction plusieurs variables | 2A | moyen | ★★★ méthodes classiques | ||||||
| problème | PROBAS | étude d’une suite infinie de pile ou face | probabilités discrètes | 1A | moyen | ★★★ TB, à faire absolument en 1A après le chapitre sur les probas | ||||||
| 2007 | correction | exercice 1 | ANALYSE | étude d’une série alternée | suites et séries numériques, développements limités | 1A | moyen | ★★★ classique, TB pour réviser les suites/DL | à faire absolument, très complet | rapport 2007 | / | |
| exercice 2 | ALGÈBRE BILI | sous-multiplicativité de la norme canonique de \(\mathcal{M}_{n}(\mathbb{R})\) | produit scalaire, matrices, diagonalisation | 2A | moyen | ★★★ | ||||||
| problème | PROBAS, ANALYSE | méthode du maximum de vraisemblance pour l’étude des paramètres d’une loi exponentielle décalée | variables à densité, fonctions de deux variables, estimation ponctuelle, covariance | 2A | difficile | ★★★ | ||||||
| 2008 | correction | exercice 1 | ALGÈBRE BILI | étude d’une famille d’endomorphismes d’un espace euclidien | espaces euclidiens, diagonalisation, projecteurs orthogonaux | 2A | moyen | ★ | à faire absolument, très complet | rapport 2008 | Le niveau moyen des copies est faible. On constate peu de progrès par rapport à l’an dernier au niveau de la présentation et de la rédaction des copies. Inutile pour un candidat de recopier les questions (en partie ou en totalité). Le manque de soin est général. Les solutions sont négligées, mal construites, bâclées, insuffisantes, bourrées d’erreurs grossières. Des résultats très importants du cours ne sont pas sus. Les candidats semblent consacrer de moins en moins de temps dans cette matière. | |
| exercice 2 | ANALYSE | étude d’une fonction définie par une série | séries numériques, fonctions d’une variable, équivalents | 1A | moyen | ★★★ classique | ||||||
| problème | PROBAS, ANALYSE | calcul approché d’une intégrale par la méthode de Monte-Carlo | VA à densité, convergence en proba, estimation par intervalle de confiance, intégrales impropres, fonction de plusieurs variables, optimisation sous contrainte d’égalité linéaire | 2A | difficile | ★★★ très complet | ||||||
| 2009 | correction | exercice 1 | ALGÈBRE BILI | diagonalisation d’un endomorphisme de \(\mathcal{M}_{n}(\mathbb{R})\) | diagonalisation, produits scalaires, endomorphismes symétriques | 2A | difficile | ★★★ | à faire absolument, TB pour réviser certaines notions précises | / | ||
| exercice 2 | ANALYSE | étude d’une fonction définie par une intégrale | intégrales impropres | 1A | moyen | TB, à faire absolument en 1A après le chapitre sur les intégrales impropres | ||||||
| problème | PROBAS, ANALYSE | étude d’une urne bicolore à la composition évolutive et à nombre de boules fixé | probas discrètes, formule de probas totales, suites | 1A | difficile | TB, à faire absolument en 1A après le chapitre sur les probas | ||||||
| 2010 | correction | exercice 1 | ANALYSE | développement asymptotique d’une suite d’intégrale | intégrales impropres, suites numériques, fonctions | 1A | moyen | ★★★ méthodes classiques | faire les deux exercices indépendamment (dans l’exercice 2 : optimisation sous contrainte non linéaire qui n’est plus au programme, mais pourrait se trouver dans un sujet HEC, si tu as bien compris, tente-le) | rapport 2010 | ||
| exercice 2 | HORS PROGRAMME : optimisation sous contrainte non linéaire | |||||||||||
| problème | PROBAS | autour du problème du collectionneur de vignettes | VA discrètes, VA à densité, suites et séries, convergence des VA | loi de Gumbel | 2A | difficile | ★★★ | |||||
| 2011 | correction | exercice 1 | ALGÈBRE BILI | algèbre linéaire et bilinéaire sur \( \mathbb R_n [X]\), polynômes d’Abel | polynômes, diagonalisation, produits scalaires | polynômes d’Abel | 2A | moyen | ★★★ | à faire absolument, notamment pour t’entraîner aux Parisiennes (notions hors programme qui reviennent souvent) | rapport 2011 | Les questions informatiques sont largement valorisées dans le barème. |
| exercice 2 | ANALYSE | étude d’une fonction de deux variables | séries, fonctions de deux variables, extrema locaux | 2A | difficile | ★★★ méthodes classiques | ||||||
| problème | PROBAS, ALGÈBRE | étude d’une suite de VA à densité et d’une équation différentielle | VA à densité, diagonalisation | maximum de VA à densité, équations différentielles | 2A | moyen | ★★★ | |||||
| 2012 | correction | exercice 1 | ANALYSE | étude et calcul d’une intégrale à paramètre | intégrales impropres, fonction d’une variable, suites implicites | 1A | moyen | ★★★ méthodes classiques | exercices à faire plutôt indépendamment en fonction de tes besoins, de meilleurs exercices existent | rapport 2012 | / | |
| exercice 2 | ALGÈBRE | étude de matrices nilpotentes | matrices, diagonalisation | 2A | difficile | ne vaut pas la peine, très calculatoire | ||||||
| problème | PROBAS, ALGÈBRE BILI | étude d’une suite de tirages dans plusieurs urnes | variables aléatoires discrètes, diagonalisation | 2A | moyen | ★★ | ||||||
| 2013 | correction | exercice 1 | ALGÈBRE BILI | propriétés des matrices dont une puissance est égale à la transposée | produits scalaires, matrices symétriques | 2A | moyen | ★★★ méthodes classiques | exercices à faire plutôt indépendamment en fonction de tes besoins, de meilleurs exercices existent (à part le 1 à faire absolument) | rapport 2013 | / | |
| exercice 2 | ANALYSE | étude d’une suite récurrente | suites, fonctions de deux variables | 2A | facile | ne vaut pas la peine | ||||||
| problème | PROBAS | discrétisées de variables aléatoires | VA discrètes, VA à densité, séries numériques, intégrales impropres | 2A | difficile | ★ très calculatoire | ||||||
| 2014 | correction | exercice 1 | ALGÈBRE | étude d’un endomorphisme d’un espace de fonctions | endomorphismes, diagonalisation | 2A | moyen | ★★★ | assez compliqué avec peu de questions classiques, mais qui reste à faire pour se préparer au plus dur | rapport 2014 | / | |
| exercice 2 | ANALYSE | calcul de la somme d’une série à l’aide de la fonction gamma | séries, intégrales impropres, inégalité de Cauchy-Schwarz | 2A | difficile | ★★★ | ||||||
| problème | PROBAS | étude d’une suite de duels à pile ou face | probabilités discrètes, suites et séries, algèbre linéaire | 1A | difficile | ★★★ | ||||||
| 2015 | correction | exercice 1 | ALGÈBRE BILI | autour des polynômes d’Hermite | algèbre bilinéaire, polynômes, diagonalisation | polynômes d’Hermite | 2A | moyen | ★★★ classique | assez intéressant, même s’il est très long, à faire pour t’entraîner à la difficulté | rapport 2015 | / |
| exercice 2 | ANALYSE | approximation de \(\pi\) par la méthode de Snellius | analyse, trigonométrie, polynômes, suites réelles | 1A | moyen | ★ | ||||||
| problème | PROBAS | espérance d’un maximum/minimum de variables aléatoires i.i.d | VA discrètes, VA à densité, lois de max/min | maximum de VA à densité | 2A | difficile | ★★★ classique, TB pour réviser les VA à densité | |||||
| 2016 | correction | exercice 1 | ANALYSE | calcul de la somme d’une série alternée | séries, intégrales, développements limités | 1A | moyen | ★★★ méthodes classiques | faire les deux exercices indépendamment (dans l’exercice 2 : optimisation sous contrainte non linéaire qui n’est plus au programme, mais pourrait se trouver dans un sujet HEC, si tu as bien compris, tente-le) | rapport 2016 | / | |
| exercice 2 | HORS PROGRAMME : optimisation sous contrainte non linéaire | |||||||||||
| problème | PROBAS, ANALYSE | étude de l’évolution du contenu d’une urne de Polya | probabilités discrètes, variables à densité, convergence en loi | 2A | moyen | ★★★ méthodes classiques | ||||||
| 2017 | correction | exercice 1 | ANALYSE | calcul de la somme d’une série alternée | intégrales, séries, fonctions d’une variable | 1A | moyen | ★★★ classique, TB pour réviser l’analyse en 1A | assez compliqué avec peu de questions classiques, mais qui reste à faire | rapport 2017 | Voir rapport tout en bas. | |
| exercice 2 | ANALYSE, ALGÈBRE BILI | optimisation de formes quadratiques et de produit de formes quadratiques sur la sphère unité | endomorphismes, fonctions N variables, optimisation sous contrainte | 2A | difficile | ★★★ méthodes classiques | ||||||
| problème | PROBAS | convergence en loi vers la loi de Rayleigh | VA discrètes, VA à densité, convergence des variables aléatoires | loi de Rayleigh | 2A | difficile | ★ très calculatoire | |||||
| 2018 | correction | exercice 1 | ALGÈBRE BILI | spectre de la composée de deux projecteurs orthogonaux | projecteurs, endomorphismes symétriques, valeurs propres | 2A | moyen | ★★★ méthodes classiques | à faire en conditions réelles pour s’entraîner à la difficulté | rapport 2018 | Rappelons que les questions informatiques sont assez largement valorisées au sein du barème de l’épreuve et que plus des deux tiers des candidats y répondent de façon suffisamment satisfaisante. | |
| exercice 2 | ANALYSE | variations autour de la suite de Fibonacci et du nombre d’or | suites, séries numériques, fonctions de plusieurs variables | 2A | moyen | ★ très calculatoire | ||||||
| problème | PROBAS, ANALYSE | algorithme de Panjer | variables aléatoires discrètes, fonctions d’une variable | algorithme de Panjer | 1A | moyen | ★★★ à faire absolument en fin de 1A | |||||
| 2019 | correction | exercice 1 | ANALYSE | étude de la suite de terme général \(I_n=\displaystyle \int_{0}^{\frac{\pi}{2}} \cos(t^n), \mathrm{d}t\) |
séries, intégrales, développements limités | 1A | moyen | ★★★ méthodes classiques | à faire absolument, très complet | rapport 2019 | Voir rapport tout en bas. | |
| exercice 2 | ALGÈBRE | vecteurs symétriques et antisymétriques | diagonalisation, sommes directes, matrices | 2A | moyen | ★★★ | ||||||
| problème | PROBAS, ALGÈBRE | étude d’un jeu de hasard avec une urne | probabilités discrètes, polynômes, application linéaire, B-T | 2A | moyen | ★★★ | ||||||
| 2020 | correction | exercice 1 | ALGÈBRE BILI | étude des polynômes de Tchebychev | polynômes, produits scalaires, trigonométrie | 2A | moyen | ★★★ méthodes classiques | à faire absolument, beaucoup de méthodes et questions classiques à ficher | rapport 2020 | Voir rapport tout en bas. | |
| exercice 2 | ANALYSE | suite des restes d’une série | intégrales, séries | 1A | difficile | ★★★ méthodes classiques | ||||||
| problème | PROBAS, ANALYSE | processus de Poisson | probabilités discrètes et à densité, développement limité | 2A | moyen | ★★★ méthodes classiques | ||||||
| 2021 | correction | exercice 1 | ALGÈBRE | étude de matrices magiques | algèbre, diagonalisation, matrices | matrices magiques | 2A | moyen | ★★★ | à faire absolument, très complet | rapport 2021 | BARÈME : les deux exercices sont de valeur sensiblement égale dans le barème : 12 à 14 points sont destinés au problème. Les candidats doivent simplifier leurs réponses aux questions de calculs, ce n’est pas au correcteur de reprendre la réponse pour en vérifier la correction ! Il est indispensable de conclure une question. |
| exercice 2 | ANALYSE | étude d’une fonction de \(\mathbb R^2\) vers \(\mathbb R : f(x,y)=(x^2+y)e^{−(x^2+y^2)}\) | fonction deux variables | 2A | difficile | ★★★ | ||||||
| problème | PROBAS | comparaison de deux estimateurs | VA à densité, estimateurs, intervalle de confiance | 2A | difficile | ★★★ | ||||||
| 2022 | correction | exercice 1 | ANALYSE | étude de la fonction polynomiale \(f(x)=\displaystyle \sum_{k=0}^{n}\frac{x^k}{k!}\) | suites, séries, intégrales, développements limités | 1A | difficile | ★★★ | à faire absolument, très complet | / | ||
| exercice 2 | ALGÈBRE | étude de la somme d’endomorphismes qui commutent, dont l’un est nilpotent et l’autre diagonalisable | diagonalisation, projecteurs | 2A | moyen | ★★★ méthodes classiques | ||||||
| problème | PROBAS, ANALYSE | autour de la loi de Gumbel | VA à densité, estimateurs | loi de Gumbel | 2A | difficile | ★★★ méthodes classiques | |||||
| 2023 | correction | exercice 1 | ALGÈBRE | étude de deux matrices \(2\times 2\) diagonalisables | matrices, diagonalisation | 2A | moyen | ★★★ méthodes classiques | à faire absolument, très complet, méthodes très classiques à ficher | / | ||
| exercice 2 | ANALYSE | étude du point critique \(m\) d’une fonction à \(n\) variables | fonction n variables, diagonalisation, endomorphismes symétriques | 2A | difficile | ★★★ méthodes classiques | ||||||
| problème | PROBAS | détermination d’un intervalle de confiance | VA à densité, estimateurs, intervalle de confiance | 2A | moyen | ★★★ méthodes classiques |
Attention aux changements de programme lorsque tu fais des annales :
Les changements de programme de maths approfondies vs ECS
Les changements de programme de maths appliquées vs ECE
Les changements de programme de maths ECT 2013 vs 2021
N’hésite pas à consulter toutes nos ressources mathématiques !