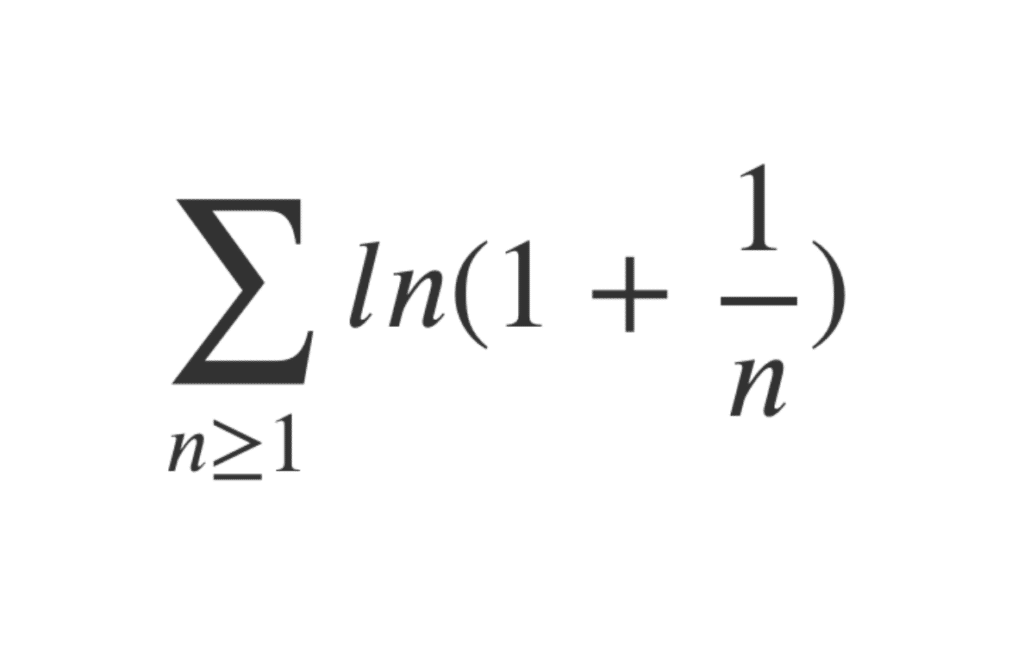En analyse, les justifications de convergence sont des questions assez redondantes, que l’on parle de séries ou d’intégrales. Elles sont également assez redondantes en probabilités, de façon un peu déguisée. Notamment lorsque l’on demande de justifier l’existence d’une espérance ou d’un moment d’ordre deux, par exemple. Il est donc important de savoir traiter de façon rigoureuse ces questions, en étant particulièrement vigilant sur les notations employées.
Dans cet article, tu trouveras une liste (presque) exhaustive des méthodes au programme pour prouver qu’une série converge. Si tu souhaites découvrir des méthodes hors programme pour prouver une convergence, je t’invite à cliquer ici.
Rappel de cours et des notations
Soit \((u_n)_{n \in \mathbb{N}}\) une suite réelle. On note \((S_n)_{n \in \mathbb{N}}\) la suite définie par :
\(\forall n \in \mathbb{N}, S_n= \displaystyle \sum_{k=0}^n u_k\).
La suite \((S_n)_{n \in \mathbb{N}}\) est appelée suite des sommes partielles.
On appelle \(\displaystyle \sum_{k \ge 0} u_k \) la série de terme général \(u_k\). On dit que cette série converge si la suite \((S_n)_{n \in \mathbb{N}}\), soit la suite des sommes partielles, converge.
Dans ce cas, on peut employer la notation \(\displaystyle \sum_{k =0}^{+ \infty} u_k \), que l’on appelle « somme de la série \(\displaystyle \sum_{k \ge 0} u_k \) », et qui désigne une valeur numérique.
Il est important de savoir jongler avec ces différents termes (série, suite des sommes partielles et somme de la série), car une confusion entre ces termes témoigne d’une connaissance imprécise du cours et sera sanctionnée.
Également, l’utilisation de la notation \(\displaystyle \sum_{k =0}^{+ \infty} u_k \) est conditionnée par une démonstration de la convergence de la série \(\displaystyle \sum_{k \ge 0} u_k \). Dit autrement, pour pouvoir écrire \(\displaystyle \sum_{k =0}^{+ \infty} u_k \), il est indispensable d’avoir démontré auparavant que la série en jeu convergeait.
Les méthodes usuelles pour démontrer la convergence d’une série
Les séries au programme
Avant de chercher à utiliser des critères de convergence, on peut déjà vérifier si la série en jeu est une série de référence. Il en existe trois : la série exponentielle, la série géométrique et ses dérivées (géométrique dérivée et géométrique dérivée seconde), et la série de Riemann.
La série exponentielle
Pour tout \(\lambda\) de \(\mathbb{R}\), la série \(\displaystyle \sum_{k \ge 0} \frac{\lambda^k}{k!} \) converge, et on a \(\displaystyle \sum_{k =0}^{+ \infty} \frac{\lambda^k}{k!}= e^{\lambda} \).
La série géométrique
Les séries \(\displaystyle \sum_{k \ge 0} q^k \) (série géométrique), \(\displaystyle \sum_{k \ge 1} k q^{k-1} \) (série géométrique dérivée) et \(\displaystyle \sum_{k \ge 2} k (k-1)q^{k-2} \) (série géométrique dérivée seconde) convergent si et seulement si \( -1 < q<1 \) et dans ce cas, on a :
\(\displaystyle \sum_{k=0}^{+\infty} q^k= \frac{1}{1-q} \), \(\displaystyle \sum_{k = 1}^{+\infty} kq^{k-1}= \frac{1}{(1-q)^2} \) et \(\displaystyle \sum_{k =2}^{+ \infty} k(k-1)q^{k-2}= \frac{2}{(1-q)^3} \).
La série de Riemann
Soit \(\alpha\), la série \(\displaystyle \sum_{n \ge 1} \frac{1}{n^{\alpha}} \) converge absolument si et seulement si \(\alpha>1\).
La série de Riemann est fondamentale, car on l’utilisera énormément pour les critères de convergence.
Refermer une somme
Si la série en jeu n’est pas l’une de ces séries, avant d’utiliser les critères de convergence, il nous reste quelque chose à tenter. En effet, l’inconvénient des critères de convergence, c’est qu’ils assurent la convergence sans donner la somme de la série.
Pour cela, avant de les utiliser, on peut essayer de « refermer la somme » de la suite des sommes partielles \((S_n)_{n \in \mathbb{R}}\). Dit autrement, on peut essayer, si c’est possible, d’exprimer, pour tout \(n\), \(S_n\) en fonction de \(n\), et non sous la forme d’une somme.
Après quoi, on pourra alors traiter la question de la convergence de la série comme une banale convergence de suite.
Certes, ce cas est assez rare, mais il faut tout de même y penser avant de se jeter sur les critères de convergence, qui restent un dernier recours ! En effet, ces critères permettent de déterminer la nature d’une série, mais jamais de donner la valeur de la somme en cas de convergence.
Les critères de convergence
Si on ne se retrouve dans aucune des situations ci-dessus, on peut alors utiliser l’un des trois critères de convergence : équivalence, négligeabilité et comparaison.
Critère d’équivalence
Commençons par rappeler le cours.
Soient \((u_n)_{n \in \mathbb{N}}\) et \((v_n)_{n \in \mathbb{N}}\) deux suites telles que \( u_n \underset{ + \infty }{\sim} v_n \). Les séries \( \displaystyle \sum_{n \ge 0} u_n\) et \( \displaystyle \sum_{n \ge 0} v_n\) sont de même nature.
Dit autrement, si l’une converge, l’autre converge également. Et si l’une diverge, l’autre diverge.
Alors, comment utiliser ce critère ?
Lorsque la question posée est de déterminer la nature de la série de terme général \(u_n\), on peut alors chercher à déterminer à équivalent simple du terme général pour se rapporter à un cas plus simple. Prenons un exemple.
Si l’on cherche à déterminer la nature de la série \( \displaystyle \sum_{n \ge 1} ln( 1 + \frac{1}{n})\), on peut utiliser cette méthode.
En effet, on a \(ln( 1 + \frac{1}{n}) \underset{ + \infty }{\sim} \frac{1}{n} \), et on sait que la série de terme général \(\frac{1}{n}\) diverge d’après le cours, car c’est une série de Riemann de paramètre 1.
Dès lors, par critère d’équivalence pour des séries à termes positifs, la série \( \displaystyle \sum_{n \ge 1} ln( 1 + \frac{1}{n})\) diverge.
Critère de négligeabilité
Soient \((u_n)_{n \in \mathbb{N}}\) et \((v_n)_{n \in \mathbb{N}}\) deux suites telles que \( u_n \underset{+ \infty}{=} \circ (v_n) \), et à termes positifs.
Alors, si la série \( \displaystyle \sum_{n \ge 0} v_n\) converge, alors la série \( \displaystyle \sum_{n \ge 0} u_n\) converge absolument.
On utilisera dans l’immense majorité des cas ce critère en se ramenant à des séries de Riemann. Prenons un exemple.
On a \( \lim \limits_{n \to +\infty} e^{-n}n^2= 0 \), donc autrement dit \( e^{-n} \underset{+ \infty}{=} \circ (\frac{1}{n^2}) \).
Or, les séries \( \displaystyle \sum_{n \ge 0} e^{-n}\) et \( \displaystyle \sum_{n \ge 0} \frac{1}{n^2}\) sont à termes positifs, et la série \( \displaystyle \sum_{n \ge 0} \frac{1}{n^2}\) converge d’après le cours, en tant que série de Riemann de paramètre 2.
Dès lors, la série \( \displaystyle \sum_{n \ge 0} e^{-n}\) converge.
Critère de comparaison
C’est le critère le plus rarement utilisé. Soient \((u_n)_{n \in \mathbb{N}}\) et \((v_n)_{n \in \mathbb{N}}\) deux suites positives telles que, à partir d’un certain rang, \(u_n \le v_n \).
Si \( \displaystyle \sum_{n \ge 0} v_n\) converge, alors \( \displaystyle \sum_{n \ge 0} u_n\) converge.
Et si \( \displaystyle \sum_{n \ge 0} u_n\) diverge, alors \( \displaystyle \sum_{n \ge 0} v_n\) diverge.
Un dernier point : la convergence absolue
J’ai volontairement laissé ce point de côté jusqu’à maintenant. Tous les critères de convergence que j’ai mentionnés nécessitent que les suites en jeu soient positives à partir d’un certain rang, ce qui est rarement le cas.
Pour contourner ce problème et faire en sorte que les suites en jeu soient bien positives, il suffit donc de rajouter des valeurs absolues. Par exemple, pour le critère d’équivalence :
si on a \((u_n)_{n \in \mathbb{N}}\) et \((v_n)_{n \in \mathbb{N}}\) deux suites telles que \( |u_n| \underset{ + \infty }{\sim} |v_n| \) et \( \displaystyle \sum_{n \ge 0} |v_n|\) converge (on dit que la série \( \displaystyle \sum_{n \ge 0} v_n\) converge absolument).
Alors, la série \( \displaystyle \sum_{n \ge 0} |u_n|\) converge, soit \( \displaystyle \sum_{n \ge 0} u_n\) converge absolument.
Et un point de ton cours te garantit que la convergence absolue entraîne la convergence (l’inverse est faux, attention…).
Dès lors, tu peux utiliser les critères de convergence en utilisant les valeurs absolues, puis finir avec la phrase suivante : « Donc, par critère de …, la série \( \displaystyle \sum_{n \ge 0} u_n\) converge absolument, donc converge. »
N’hésite pas à consulter toutes nos ressources en mathématiques !