En plus des fonctions trigonométriques classiques qui sont au programme, il en existe d’autres qui tombent parfois aux concours, comme les fonctions sinh (ou sh) et cosh (ou ch) appelées également cosinus hyperbolique et sinus hyperbolique. Dans cet article, tu trouveras des astuces sur ces deux fonctions, qui sont tombées l’année dernière dans le sujet EDHEC 2022.
Les fonctions de trigonométrie dites hyperboliques
Sans répéter l’article concernant les fonctions trigonométriques (qui sont au programme en ECG), voici tout d’abord les bases à connaître sur ces deux fonctions.
Le cosinus hyperbolique
Le cosinus hyperbolique est la partie paire de la fonction exponentielle. Il est noté \(ch\) et est défini par
\(\displaystyle ch(x)=\frac{e^{x}+e^{-x}}{2}\)
La fonction cosh (ou ch) est une application de ℝ dans [1, +∞[ strictement croissante sur ℝ+, et paire. La fonction cosh est de classe C∞ sur ℝ et sa dérivée est le sinus hyperbolique.
Le sinus hyperbolique
Le sinus hyperbolique est la partie impaire de la fonction exponentielle. Il est noté \(sh\) et est défini par
\(\displaystyle sh(x)=\frac{e^{x}-e^{-x}}{2}\)
La fonction sinh (ou sh) est une bijection de classe C∞ de ℝ sur ℝ strictement croissante et impaire. Sa dérivée est le cosinus hyperbolique.
Démonstrations de résultats classiques autour de cosh et sinh
Une fois les fonctions bien définies, passons à la réponse de questions classiques.
Parité
- La fonction \(ch\) est paire
En effet, \(\displaystyle \forall x \in \mathbb{R}, -x \in \mathbb{R}\) et \(\displaystyle \forall x \in \mathbb{R}, ch(-x)=\frac{e^{-x}+e^{x}}{2}=ch(x)\)
Donc, \[ \fbox{ ch est paire }\]
- La fonction \(sh\) est impaire
En effet, \(\displaystyle \forall x \in \mathbb{R}, -x \in \mathbb{R}\) et \(\displaystyle \forall x \in \mathbb{R}, sh(-x)=\frac{e^{-x}-e^{x}}{2}=-sh(x)\)
Donc, \[ \fbox{ sh est impaire }\]
Dérivées
- La dérivée de \(ch\) est \(sh\)
En effet, la fonction \(ch\) est dérivable sur \(\mathbb{R}\) et \(\forall x \in \mathbb{R}\), on a :
\(\displaystyle ch'(x)=\frac{e^{x}+(-e^{-x})}{2}=\frac{e^{x}-e^{-x}}{2}=sh(x)\)
- La dérivée de \(sh\) est \(ch\)
En effet, a fonction \(sh\) est dérivable sur \(\mathbb{R}\) et \(\forall x \in \mathbb{R}\), on a :
\(\displaystyle sh'(x)=\frac{e^{x}-(-e^{-x})}{2}=\frac{e^{x}+e^{-x}}{2}=ch(x)\)
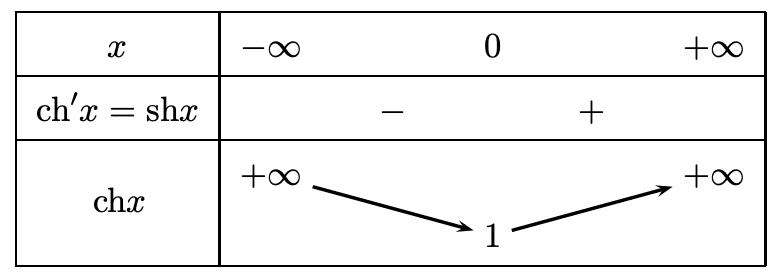
Variations
- La fonction \(ch\) est décroissante sur \(\mathbb{R}^{-}\) et croissante sur \(\mathbb{R}^{+}\)
Le domaine d’étude de la fonction \(ch\) se réduit à [0, +∞[ puisqu’il s’agit d’une fonction paire.
\(\displaystyle \forall x \in \mathbb{R}, ch'(x)=sh(x)\ge 0\),
donc la fonction \(ch\) est croissante sur [0, +∞[ et ainsi par parité, décroissante sur ]\(-\infty,0]\)
De plus, \(ch(0)=1 \) et \(\lim \limits_{x \to +\infty} ch(x)=+\infty\)
D’où le tableau de variation suivant :
- La fonction \(sh\) est strictement croissante sur \(\mathbb{R}\)
Il suffit de l’étudier sur [0, +∞[ puisqu’il s’agit d’une fonction impaire. La dérivée de \(sh\) est \(ch\) et on a vu que \(ch x > 0\) pour tout x ∈\(\mathbb{R}\), donc \(sh\) est strictement croissante.
D’où le tableau de variation suivant :

Bijections réciproques
- La fonction \(ch\) est continue et strictement croissante sur [0, +∞[, elle réalise donc une bijection de cet intervalle sur son image [1, +∞[ et on peut définir son application réciproque.
On appelle fonction argument cosinus hyperbolique, et on note \(argch\) la fonction
\(argch : \begin{cases} [1, +∞[ \to [0, +∞[, \\
x \mapsto argch(x) \end{cases}\)
l’application réciproque de la restriction de la fonction cosinus hyperbolique à l’intervalle [0, +∞[
Calculons l’expression de \(argch\)
\(\forall x \ge 1\), on résout l’équation \(\displaystyle y=ch(x) \Leftrightarrow y= \frac{e^x+e^{-x}}{2} \Leftrightarrow 2y=e^{x}+e^{-x} (e^{x})^{2}-2ye^{x}+1=0\) en multipliant par \(e^{x}\)
D’où :
\(\displaystyle y=ch(x)\Leftrightarrow\begin{cases} X=e^{x} \\X^{2}-2yX+1=0 \end{cases}\Leftrightarrow\begin{cases} \displaystyle X=e^{x} \\X=\frac{2y\pm\sqrt{4y^{2}-4}}{2}=y\pm\sqrt{y^{2}-1}\end{cases}\)
Or, \(\displaystyle y-\sqrt{y^{2}-1}\le 0\) donc la seule solution possible est \(\displaystyle X=y+\sqrt{y^{2}-1}\)
Finalement, on a :
\(\displaystyle y=ch(x)\Leftrightarrow x=\ln(y+\sqrt{y^{2}-1})\)
Ce qui signifie que :
\[ \fbox{\( \displaystyle argch(y)=\ln(y)+\sqrt{y^{2}-1}\)}\]
- La fonction \(sh\) est continue et strictement croissante sur R, elle réalise donc une bijection de cet intervalle sur son image R et on peut définir son application réciproque.
On appelle fonction argument sinus hyperbolique et on note \(argsh\) la fonction
\(argsh : \begin{cases} R \to R, \\
x \mapsto argsh(x) \end{cases}\)
l’application réciproque de la fonction sinus hyperbolique.
Calculons l’expression de \(argsh\)
\(\forall x \ge 1\), on résout l’équation \(\displaystyle y=sh(x) \Leftrightarrow y= \frac{e^{x}-e^{-x}}{2} \Leftrightarrow 2y=e^{x}-e^{-x} (e^{x})^{2}-2ye^{x}-1=0\) en multipliant par \(e^{x}\)
D’où :
\(
y=ch(x)
\Leftrightarrow
\begin{cases} X=e^{x} \\
X^{2} -2yX-1=0 \end{cases} \Leftrightarrow \begin{cases} X=e^{x} \\ X=\displaystyle \frac{2y\pm\sqrt{4y^{2}+4}}{2}=y\pm\sqrt{y^{2}+1} \end{cases}\)
Or, \(\displaystyle y-\sqrt{y^{2}+1}\le 0\) donc la seule solution possible est \(\displaystyle X=y+\sqrt{y^{2}+1}\)
Finalement, on a :
\(
y=sh(x)
\Leftrightarrow
x=\ln(y+\sqrt{y^{2}+1})\)
Ce qui signifie que :
\[ \fbox{\( \displaystyle argsh(y)=\ln(y)+\sqrt{y^{2}+1}\)}\]
Équivalent
Un résultat classique à savoir démontrer est l’équivalent : \(sh(x) \underset{0}{\sim}x\)
D’après le cours :
\(e^{x}\underset{0}{=} 1+x+o(x)\)
et \(e^{-x}\underset{0}{=} 1-x+o(x)\)
Donc :
\(\displaystyle \frac{e^{x}-e^{-x}}{2}\underset{0}{=} x+o(x) \)
donc \(\displaystyle \frac{e^{x}-e^{-x}}{2x}\underset{0}{=} 1+o(1)\)
D’où \(\displaystyle \lim \limits_{x\to 0}\frac{e^{x}-e^{-x}}{2x}=1 \)
D’où \(\displaystyle \lim \limits_{x\to 0}\frac{\frac{e^{x}-e^{-x}}{2}}{x}=1 \)
Donc, finalement, on a : \[ \fbox{\( \displaystyle sh(x) \underset{0}{\sim}x \)}\]
Propriétés
Un résultat classique à savoir démontrer est l’égalité : \(\forall x \in \mathbb{R}, ch^{2}(x)-sh^{2}(x)=1\)
En effet, \(\displaystyle \forall x \in \mathbb{R}, ch^{2}(x)-sh^{2}(x)=(\frac{e^{x}+e^{-x}}{2})^{2}-(\frac{e^{x}-e^{-x}}{2})^{2}=\frac{(e^{x})^{2}+2e^{x}e^{-x}+(e^{-x})^{2}}{4}-\frac{(e^{x})^{2}-2e^{x}e^{-x}+(e^{-x})^{2}}{4}=\frac{4e^{x}e^{-x}}{4}=1\)
D’où, finalement, \[ \fbox{\( \displaystyle \forall x \in \mathbb{R}, ch^{2}(x)-sh^{2}(x)=1\)}\]
Illustration des fonctions trigonométriques hyperboliques cosh et sinh
Tout comme la fonction \(\arctan\), on étudie parfois les fonctions réciproques de \(cos\) et \(sin\) que sont respectivement les fonctions \(\arccos\) et \(\arcsin\).
De même, bien que ce soit surtout des notions étudiées par les prépas scientifiques, il arrive parfois que les concepteurs des épreuves de maths des prépas commerce s’amusent à utiliser les fonctions des cosinus et sinus hyperboliques. Elles sont définies comme suit :
\(\forall x \in \mathbb{R}, ch(x)=\frac{e^{x}+e^{-x}}{2}\)
\(\forall x \in \mathbb{R}, sh(x)=\frac{e^{x}- e^{-x}}{2}\)
Voici un petit graphique pour t’aider à comprendre (le sinus hyperbolique est représenté en orange et le cosinus hyperbolique en bleu) :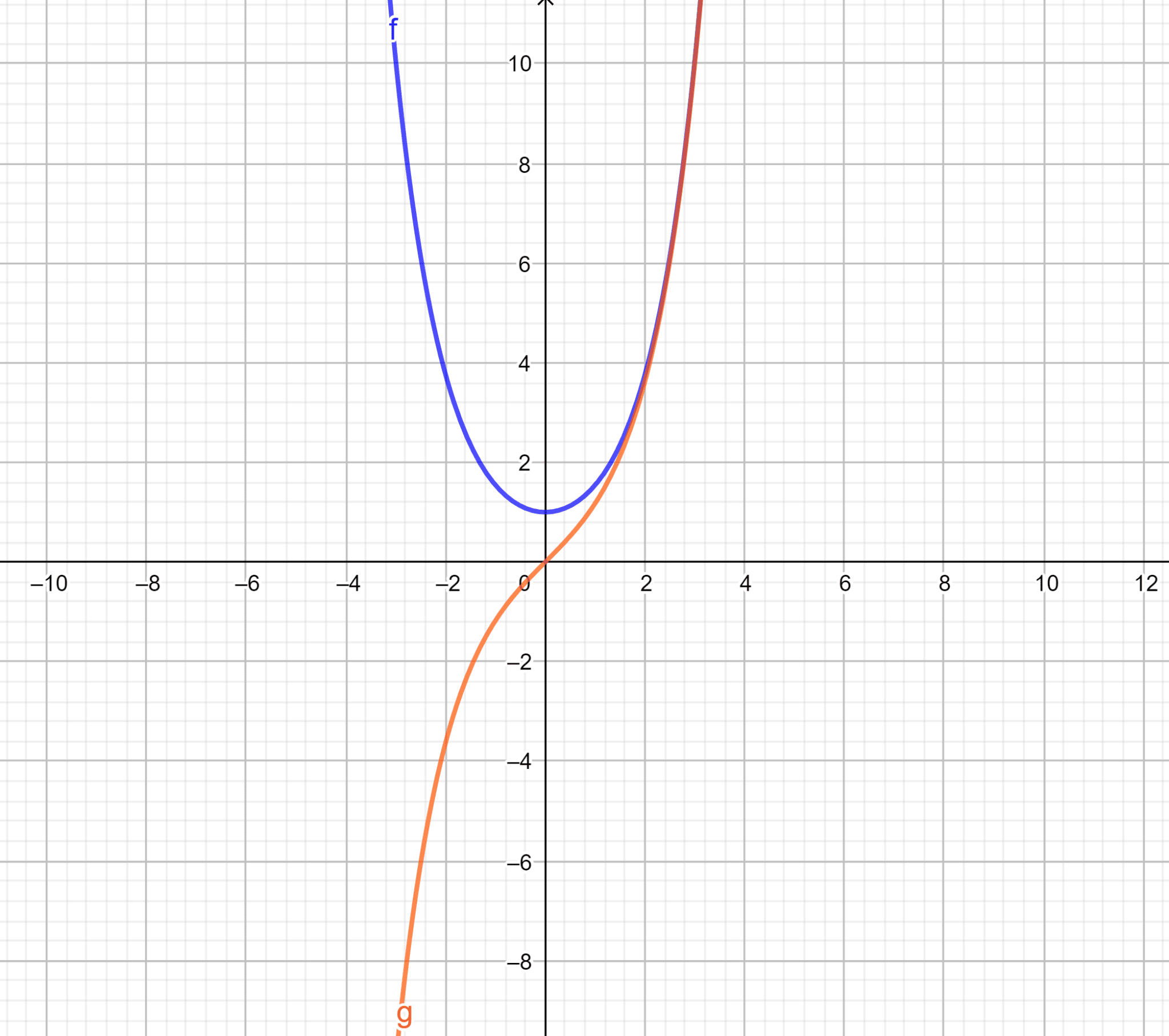
Illustration des domaines de définition du cosinus et du sinus hyperbolique
En réalité, les fonctions \(\arccos\) et \(\arcsin\) sont les fonctions réciproques de \(cos\) et \(sin\) restreintes à certains intervalles. Ainsi, \(\arccos\) est la fonction réciproque de la fonction \(cos\) restreinte à l’intervalle \([0,\pi]\).
La fonction \(\arcsin\) est, elle, la fonction réciproque de la fonction \(sin\) restreinte à l’intervalle \([- \frac{\pi}{2}, \frac{\pi}{2}]\).
Ainsi, les fonctions \(\arccos\) et \(arcsin\) sont toutes les deux définies et continues sur l’intervalle \([-1,1]\) et à valeurs respectivement dans \([0, \pi]\) et \([- \frac{\pi}{2}, \frac{\pi}{2}]\).
Tu peux t’aider de ce graphique pour mieux les visualiser, \(\arccos\) est représentée en vert et \(\arcsin\) en rouge : 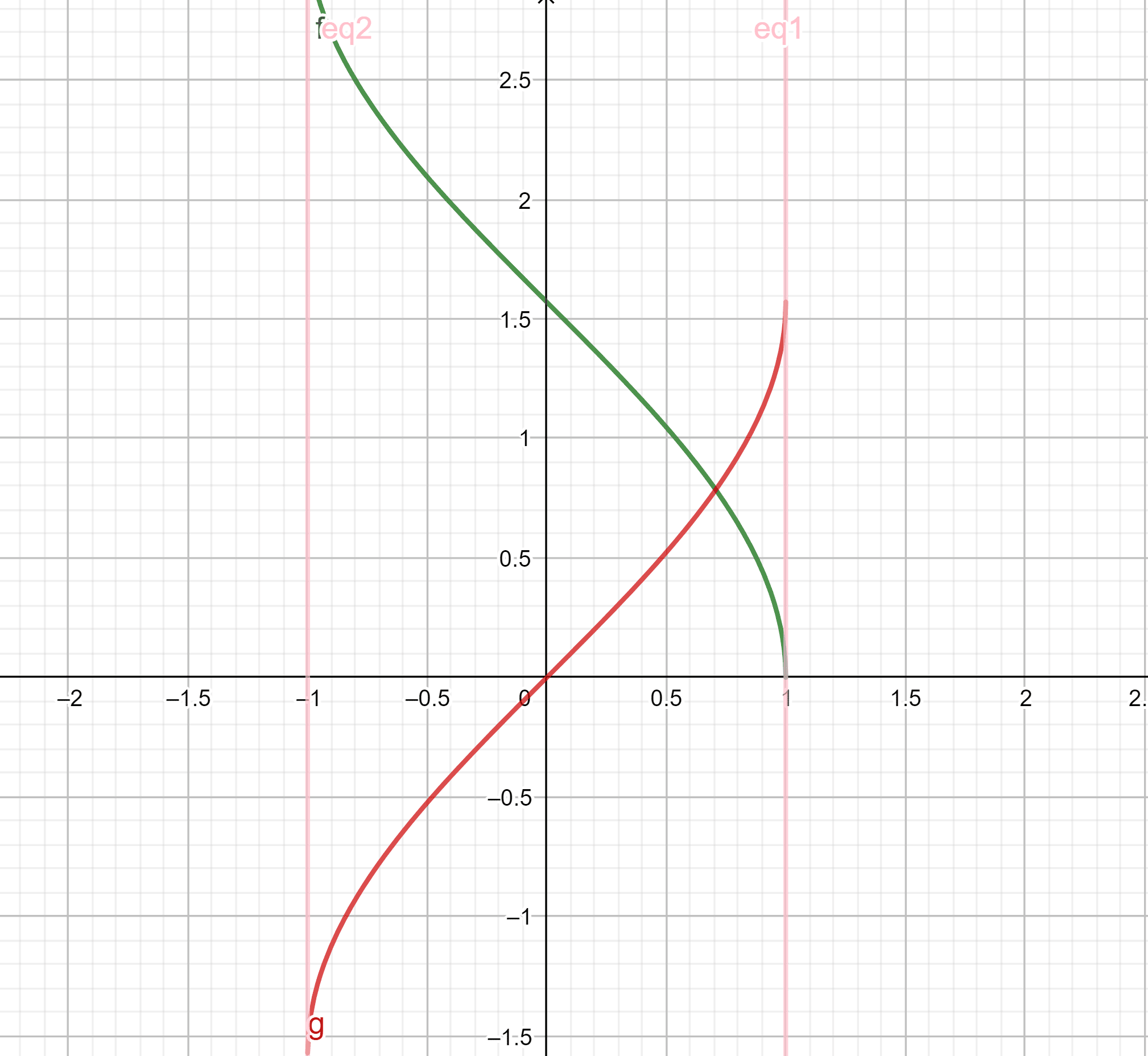
Les deux fonctions hyperboliques sont quant à elles toutes les deux définies sur \(\mathbb{R}\).
Les formules à connaître autour de cosh et sinh
Avant toute chose, un petit rappel sur ce que signifie en mathématiques le fait d’être la fonction réciproque d’une autre fonction.
C’est tout simplement que \(\forall x \in [0, \pi], \arccos(\cos(x)) = x \). Ainsi, de même, on a : \(\forall x \in [- \frac{\pi}{2}, \frac{\pi}{2}], \arcsin(\sin(x)) = x\).
Enfin, si tu veux pouvoir avancer facilement dans un sujet qui fait appel aux fonctions trigonométriques hors programme et avoir des outils pour le comprendre, il est important que tu retiennes ces quelques formules :
- \(\forall x \in [-1,1], \arccos(-x) = \pi – \arccos(x)\)
- \(\sin(\arccos(x)) = \left (\sqrt(1- x^2)\right) \)
- \(\cos(\arcsin(x)) = \left (\sqrt(1- x^2)\right) \)
- \(\forall x\in [-1, 1], \arccos(x) + \arcsin(x) = \frac{\pi}{2} \)
Concernant les \(cosinus\) et \(sinus\) hyperboliques, il existe également de nombreuses formules différentes, mais voici celles que tu dois connaître :
- \(\forall x \in \mathbb{R}, ch(x)^2 – sh(x)^2 = 1\)
\(\forall (a,b) \in \mathbb{R}^{2}\) :
- \(sh(a + b) = sh(a).ch(b) + sh(b).ch(a)\)
- \(ch(a+b) = ch(a).ch(b) + sh(a).sh(b)\)
Tu sais tout sur les fonctions trigonométriques ! À présent, si tu veux aller plus loin et maîtriser d’autres notions hors programme qui reviennent régulièrement, voici quelques faits pour toi :
Les matrices magiques (hors programme ECG)
Matrice compagnon (hors programme ECG)
La trigonométrie expliquée dans une vidéo très complète
Si des paroles sont mieux que des mots pour ta compréhension de la trigonométrie, on t’invite à aller voir cette merveilleuse vidéo explicative de Ambroise réalisée sur notre chaîne youtube, il détaille vraiment tout sur tout de la trigonométrie dans les moindres détails…
Aller plus loin
Les fonctions de trigonométries peuvent être approfondies sous différentes formes. En effet, les fonctions sinus et cosinus ont donné lieu à de nombreuses notions hors programme (qui se trouvent régulièrement dans les sujets). Parmi elles, tu peux retrouver : voici un tableau récapitulatif de toutes nos ressources de trigonométrie sur Major Prépa, que ce soit aussi bien en termes de notions de cours comme de notions hors programme :
| Contenu de trigonométrie au programme et hors programme ECG | |
| Trigo au programme | Trigo hors programme |
| Tout sur les fonctions de trigonométrie cos et sin | Les fonctions de trigonométrie cosh et sinh (cosinus hyperbolique et sinus hyperbolique) |
| Fiche récapitulative des formules de trigo | Trigonométrie et nombres complexes |
| Démonstrations des formules trigonométriques | La loi arcsinus standard et à support borné |
| Zoom sur la fonction Arctangente (Arctan et toutes ses méthodes associées) | Les intégrales de Wallis |
| Vidéo explicative de la trigonométrie | L’intégrale de Dirichelet |
| La trigonométrie (du point de vue du lycée, trigo troisième, trigonométrie en seconde…) | Transformée de Fourier (mais il y a des nombres complexes…) |
| Tout comprendre sur le cercle trigonométrique | |
Si tu veux aller plus loin dans les fonctions de trigonométrie hyperboliques sinh et cosh, entraîne-toi avec le sujet EDHEC 2022. N’hésite pas à consulter toutes nos ressources mathématiques.












