Hello! Aujourd’hui, focus sur une notion hors programme, dont tu as forcément déjà entendu parler : la suite de Fibonacci. Cet article s’adresse à tous les curieux. Alors, bizuth ou carré, à toi de jouer 😉
Présentation
La suite de Fibonacci est une suite d’entiers définie par \(F_0=0\), \(F_1=1\) et \(\forall n \ge 2, F_n=F_{n-1}+F_{n-2}\).
Les premiers termes sont ainsi 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, etc.
Un peu d’histoire
Au XIIIᵉ siècle, Leonardo Fibonacci (qui a donné son nom à la suite, comme tu l’auras compris) s’est penché sur un problème un peu enfantin dans son livre Liber abaci : « Quelqu’un a déposé un couple de lapins dans un certain lieu, clos de toutes parts, pour savoir combien de couples seraient issus de cette paire en une année, car il est dans leur nature de générer un autre couple en un seul mois, et qu’ils enfantent dans le second mois après leur naissance. »

On admet pour ce problème que les couples en âge de procréer se reproduisent chaque fois et qu’aucun lapereau ne meurt jamais.
Après le premier et le deuxième mois, il y a un couple seulement de lapins, puisque les premières naissances n’ont pas encore eu lieu. Après trois mois, un nouveau couple est né, mais celui-ci ne peut pas encore procréer. Le premier couple attend quant à lui une nouvelle portée. Après quatre mois, on assiste à la naissance de deux nouveaux lapereaux et au début de la gestation des deux femelles des couples précédents. On compte donc à l’issue du cinquième mois, cinq couples de lapins. Et ainsi de suite…
En continuant ainsi l’observation, on peut poser l’hypothèse que le nombre de couples de lapins au mois \(n\) est égal à la somme du nombre de couples de lapins au mois \(n-1\) et du nombre de couples de lapins au mois \(n-2\).
Géométrie
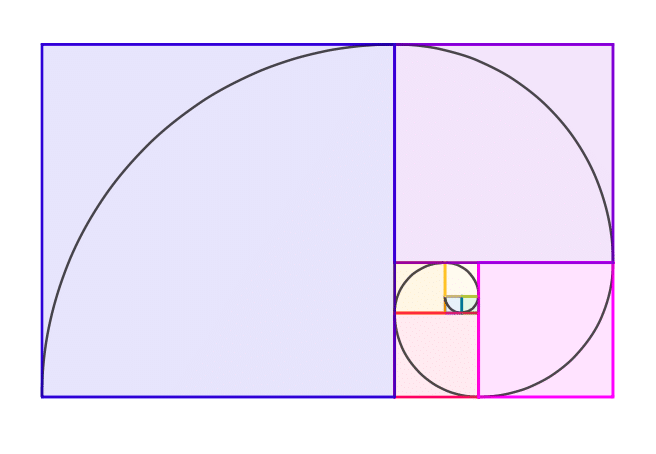
Normalement, la suite de Fibonacci doit t’évoquer une spirale. En effet, c’est elle qui permet de modéliser de nombreuses figures que l’on retrouve dans la nature, comme la coquille d’un escargot, la ramification des arbres ou dans la manière dont sont organisés les nuages dans l’œil d’un cyclone.

Pour obtenir cette spirale, on construit peu à peu des carrés de côté \(F_n\) avec \(n \in \mathbb{N}\).
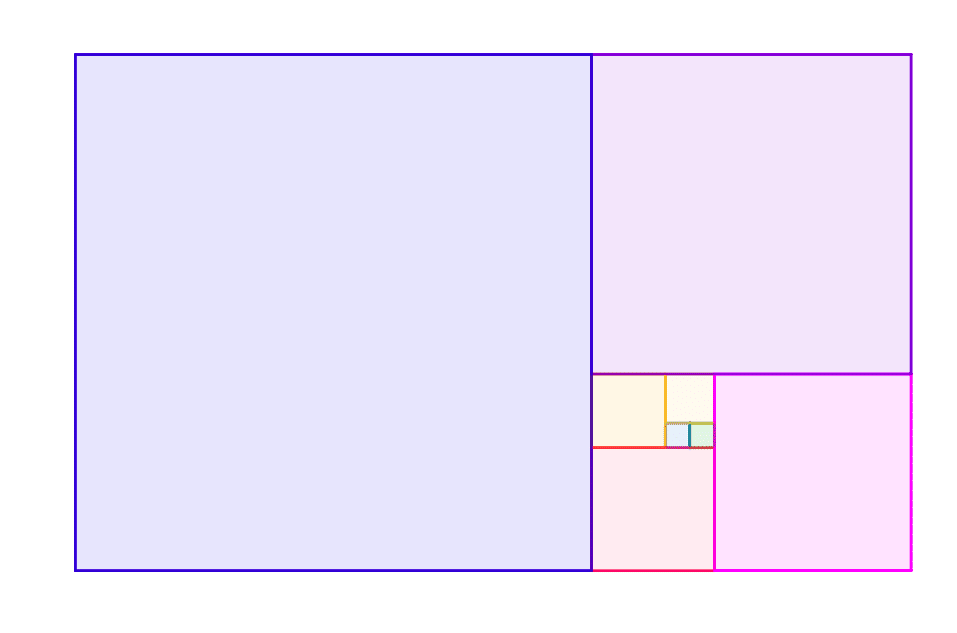
On relie ensuite les sommets des carrés pour avoir la spirale tant attendue.
Nombre d’or
La suite telle que définie par Fibonacci est facile à utiliser, mais (problème !) tu as toujours besoin des termes précédents. Les recherches successives de Moivre, Euler et Binet ont toutefois montré qu’on pouvait tirer de la formule de récurrence une expression fonctionnelle, ne dépendant plus que de \(n\), que l’on appelle formule de Binet :
\(\forall n \in \mathbb{N}, F_n=\frac{1}{\sqrt 5} (\phi^n – \phi’^n)\) avec \(\phi=\frac{1+\sqrt5}{2}\) et \(\phi’=\frac{1-\sqrt5}{2}=\frac{1}{\phi}\).
On peut bien sûr montrer la formule de Binet par une récurrence double.
On peut alors remarquer que \(F_n \underset{+\infty}{\sim}\frac{\phi^n}{\sqrt5}\) et on en déduit que le taux de croissance des nombres de Fibonacci (\(\frac{F_{n+1}}{F_n}\)) converge vers \(\phi\).
\(\phi\) est appelé « nombre d’or ». Ce nombre est associé à de nombreuses qualités esthétiques au sein de notre civilisation. En effet, il est solution de l’équation \(x^2=x+1\) (tu peux le vérifier), ce qui crée un rapport équilibré dans les proportions dont l’œil humain raffole.
Il a ainsi été employé par les Grecs pour décider de la dimension du fronton du Panthéon, ou bien encore utilisé par Léonard de Vinci pour décider des rapports de taille dans La Joconde et L’Homme de Vitruve.

Maintenant, revenons-en aux mathématiques !
Expression matricielle
Très souvent, l’expression des termes d’une suite peut être trouvée avec l’aide des matrices. La suite de Fibonacci n’échappe pas à la règle.
On a assez facilement \(\begin{pmatrix} F_n \\ F_{n-1} \end{pmatrix} = \begin{pmatrix} 1 & 1 \\ 1
& 0\end{pmatrix} \begin{pmatrix} F_{n-1} \\ F_{n-2} \end{pmatrix}\). Par itération, on obtient \(\begin{pmatrix} F_n \\ F_{n-1} \end{pmatrix} = \begin{pmatrix} 1 & 1 \\ 1 & 0\end{pmatrix}^n \begin{pmatrix} 0 \\ 1 \end{pmatrix}\).
De la même façon, \(\begin{pmatrix} F_{n+1} \\ F_{n} \end{pmatrix} = \begin{pmatrix} 1 & 1 \\ 1 & 0\end{pmatrix}^n \begin{pmatrix} 1 \\ 0 \end{pmatrix}\).
On en déduit que \(\begin{pmatrix} F_{n+1} & F_n \\ F_n & F_{n-1} \end{pmatrix} = \begin{pmatrix} 1 & 1 \\ 1 & 0\end{pmatrix}^n\).
Un logiciel pourra ainsi te donner facilement la valeur de \(F_n\). Rappelle-toi aussi que les matrices sont souvent bien plus simples à manipuler.
Lien avec les espaces vectoriels
Tu peux aussi retrouver la suite de Fibonacci dans des exercices d’algèbre linéaire puisque, finalement, cette suite n’est rien de plus qu’une suite récurrente linéaire d’ordre 2.
Elle est à l’origine d’un sous-espace vectoriel. En effet, soit \(\epsilon={(u_n)_{n \in \mathbb{N}} \in \mathbb{R}^{\mathbb{N}}, u_{n+2}=u_{n+1}+u_n}\), alors pour tout \((u_n) \in \mathbb{R}^{\mathbb{N}}, \exists! (a, b) \in \mathbb{R}^2\) tel que \(u_n=aF_n +bF_{n+1}\).
Une base de \(\epsilon\) est donc \(((F_n), (F_{n+1}))\).
Et voilà le plus important à propos de la suite de Fibonacci ! J’espère que cet article t’a plu, tu peux consulter toutes nos autres ressources de mathématiques en cliquant ici.










