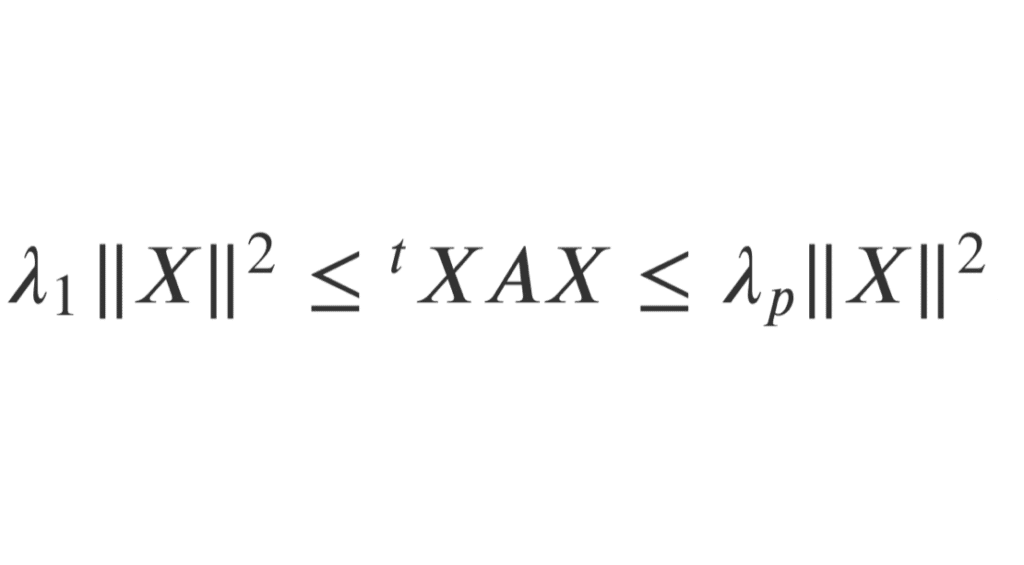Les questions d’algèbre bilinéaire varient généralement beaucoup d’un sujet à un autre. Malgré tout, il existe des questions qui se retrouvent dans presque tous les sujets.
Parmi ces dernières, la question star de l’algèbre bilinéaire est l’encadrement de Rayleigh. Cette question est par exemple posée dans le sujet HEC 2006 maths 1 à la question 2) b) de la Partie I (tu trouveras le lien du sujet ici), ou encore dans le sujet ESSEC 2005 maths 1 à la question 2) a) de la Partie II (tu trouveras le lien du sujet ici).
L’encadrement de Rayleigh est à la limite du programme. Certains considèrent même qu’il s’agit d’un point de cours ! Il est donc indispensable de savoir le démontrer rapidement, presque par cœur, et sous ses différentes formes. Pour cela, je te propose différentes méthodes pour gagner du temps sur cette question incontournable.
Attention, cet article est un article spécial maths approfondies. La théorie de l’algèbre bilinéaire n’est pas au programme des maths appliquées.
Soit \(n \in \mathbb N^*\).
Le résultat
L’encadrement de Rayleigh existe sous deux formes. L’une est dite matricielle et l’autre vectorielle. Ces résultats se ressemblent, mais leur démonstration diffère.
La version matricielle
Soit \(A\) une matrice symétrique de \(\mathcal{M}_n(\mathbb{R})\). En notant \(\lambda_1, \dots, \lambda_p\) ses valeurs propres telles que \(\lambda_1 \le \dots\le \lambda_p\), on a :
\(\forall X \in \mathbb{R}^n, \lambda_1\|X\|^2 \le {}^t X AX \le \lambda_p \|X\|^2\), où \(\|\dots\|\) désigne la norme euclidienne canonique de \(\mathbb{R}^n\).
La version vectorielle
Soit \(E\) un espace vectoriel euclidien de dimension \(n\), et \(f\) un endomorphisme symétrique de \(E\). En notant \(\lambda_1, \dots, \lambda_p\) ses valeurs propres telles que \(\lambda_1 \le \dots\le \lambda_p\), on a :
\(\forall x \in E, \lambda_1\|x\|^2 \le \langle f(x), x \rangle \le \lambda_p \|x\|^2\).
Remarque
Tu pourrais te demander pourquoi on peut affirmer sans problème que les valeurs propres \(\lambda_i\) existent. Sur ce point, tu n’as pas à t’inquiéter : c’est garanti par le cours.
En effet, d’après le théorème spectral, on sait qu’une matrice symétrique \(A\) de \(\mathcal{M}_n(\mathbb{R})\) est diagonalisable, et même qu’il existe une matrice \(P\) orthogonale et une matrice \(D\) diagonale, dont les coefficients diagonaux sont les valeurs propres telles que \(A={}^t P DP\).
De même, toujours d’après le théorème spectral, si \(f\) est un endomorphisme symétrique de \(E\), alors \(f\) est diagonalisable (ce théorème affirme même que \(f\) est diagonalisable dans une base orthonormale de \(E\)). Naturellement, \(f\) possède bien des valeurs propres.
Ce fameux théorème spectral est en fait le pilier de la démonstration de l’encadrement de Rayleigh.
Comment prouver l’encadrement de Rayleigh ?
La méthode matricielle
Pour prouver rapidement cet encadrement, appliquer le théorème spectral reste la méthode la plus efficace et élégante.
On sait que \(A\) est une matrice symétrique de \(\mathcal{M}_n(\mathbb{R})\), donc d’après le théorème spectral, il existe une matrice \(P\) orthogonale et une matrice \(D\) diagonale, dont les coefficients diagonaux sont les valeurs propres de \(A\) (On note \(D=diag(\mu_1, \dots, \mu_n)\), où les \(\mu_i\) sont les \(\lambda_i\), mais potentiellement comptés plusieurs fois, en fonction de la dimension du sous-espace propre associé à la valeur propre \(\lambda_i\)), telles que \(A={}^t PDP\).
Soit \(X \in \mathbb{R}^n\), on a :
\({}^t X AX={}^t X{}^t PDPX={}^t (PX) D (PX)\).
A priori, cette nouvelle écriture ne nous aide pas énormément. Et pourtant, le fait que la matrice au centre ne soit plus \(A\) mais \(D\), une matrice diagonale, ça change tout ! En effet, cela va largement faciliter nos calculs. Si l’on note \(Y=PX\), on a donc :
\({}^t XAX= {}^t Y DY\).
Et en notant \(Y=(y_1, \dots, y_n)\), on a après calcul (un produit matriciel classique) :
\(DY=\begin{pmatrix} \displaystyle \sum_{i=1}^{n}\mu_1y_i
\\ \displaystyle \sum_{i=1}^{n}\mu_2y_i& \\ \vdots \\ \displaystyle \sum_{i=1}^{n}\mu_ny_i
\end{pmatrix}\).
Et en multipliant à gauche par \({}^t Y\), \({}^t Y DY=\displaystyle \sum_{i=1}^{n}\mu_iy_i^2\).
Or, on sait que \(\forall i \in [\! [1,n]\!], \lambda_1 \le \mu_i \le \lambda_p\), donc \(\forall i \in [\! [1,n]\!], \lambda_1y_i^2 \le \mu_i y_i^2\le \lambda_py_i^2\), car \(y_i^2\) est positif.
Alors, en sommant, par linéarité de la somme, et en rappelant que \(\displaystyle \sum_{i=1}^{n}y_i^2=\|Y\|^2\), on a :
\(\lambda_1 \|Y\|^2\le {}^t Y DY\le \lambda_p\|Y\|^2\), soit encore \(\lambda_1 \|Y\|^2\le {}^t X AX\le \lambda_p\|Y\|^2\).
Cela ressemble énormément à ce que l’on doit trouver. Simplement, le \(\|Y\|^2\) doit être remplacé par \(\|X\|^2\).
Mais en fait, on retombe sur nos pattes puisque \(\|Y\|^2={}^tYY={}^t(PX)PX={}^tX{}^tPPX={}^tXX=\|X\|^2\) (car rappelle-toi, \(P\) est orthogonale, donc \({}^tPP=I_n\)).
Ainsi, on a bien montré que \(\lambda_1 \|X\|^2\le {}^t X AX\le \lambda_p\|X\|^2\).
La méthode vectorielle
Soient \(E\) un espace vectoriel euclidien de dimension \(n\) et \(f\) un endomorphisme symétrique de \(E\). On note de la même façon que pour la méthode matricielle les \(\mu_i\), les valeurs propres de \(f\).
Comme pour la méthode matricielle, le point de départ de notre raisonnement est le théorème spectral, dans sa version vectorielle cette fois-ci.
Comme \(f\) est un endomorphisme symétrique, il existe une base orthonormale de \(E\) formée de vecteurs propres de \(f\). On la note \(\mathcal{B}(=e_1, \dots, e_n)\), où \(\forall i \in [\![1,n]\!], f(e_i)=\mu_ie_i\).
Soit \(x \in E\). On va alors pouvoir exploiter la base que l’on a définie. On a : \(\exists! (x_i)_{1 \le i \le n} \in \mathbb{R}^n | x=\displaystyle \sum_{i=1}^{n}x_ie_i\). Et de plus, comme \(\mathcal{B}\) est une base orthonormale de \(E\), \(\|x\|^2=\displaystyle \sum_{i=1}^{n}x_i^2\).
Il ne nous reste plus qu’à exploiter ces différentes informations.
\(\langle f(x),x \rangle=\langle f(\displaystyle \sum_{i=1}^{n}x_ie_i), \displaystyle \sum_{j=1}^{n}x_je_j\rangle=\langle\displaystyle \sum_{i=1}^{n}x_if(e_i),\displaystyle \sum_{j=1}^{n}x_je_j \rangle\) par linéarité de \(f\).
Puis, comme \(\forall i \in [\![1,n]\!], f(e_i)=\mu_ie_i\), on a :
\(\langle f(x),x \rangle=\langle\displaystyle \sum_{i=1}^{n}x_i\mu_ie_i, \displaystyle \sum_{j=1}^{n}x_je_j \rangle\).
Par bilinéarité du produit scalaire et comme la famille \(\mathcal{B}\) est orthonormale, il vient alors :
\(\langle f(x),x \rangle=\displaystyle \sum_{i=1}^{n} \displaystyle \sum_{j=1}^{n}\mu_ix_ix_j\ \langle e_i,e_j\rangle=\displaystyle \sum_{i=1}^{n} \mu_ix_i^2\).
Il ne reste plus qu’à conclure en raisonnant exactement comme ci-dessus, à partir de l’encadrement \(\forall i \in [\![1,n]\!], \lambda_1 \le \mu_i \le \lambda_p\), tout en rappelant que \(\|x\|^2=\displaystyle \sum_{i=1}^{n}x_i^2\).
N’hésite pas à consulter toutes nos autres ressources de maths !
