Beaucoup de notions se cachent derrière le terme topologie, qui est un peu obscur et, depuis longtemps, à la limite du programme. À ce problème, certains concepteurs de sujets parisiens ont une réponse facile : introduire les notions hors programme au début d’un sujet. Cela leur permet de pouvoir poser des questions de topologie aux étudiants.
Il est donc nécessaire, pour tout préparationnaire qui vise une Parisienne, de se frotter au moins une fois à la topologie. Histoire de ne pas se retrouver perdu dans des sujets devenus aujourd’hui mythiques, comme HEC Maths 1 2010 (sujet ici) ou HEC 2002 Maths 1 (énoncé).
Je te propose donc un tour d’horizon des différentes questions qui peuvent être posées aux concours abordant des notions de topologie.
Attention, cet article s’adresse uniquement aux étudiants en maths approfondies et qui visent clairement une école parisienne.
Les outils du cours en topologie
Contrairement à une croyance assez généralisée, nous ne sommes pas démunis en topologie si l’on utilise uniquement les notions de cours. Le cours nous offre quelques outils pour appréhender la notion de fermés et d’ouverts. Notion absolument fondamentale lorsque l’on pratique l’optimisation (tu trouveras un article sur l’optimisation ici).
Les définitions
Un ouvert de \(\mathbb{R}^n\)
On dit que \(\Omega\) une partie de \(\mathbb{R}^n\) est un ouvert lorsque :
\(\forall a \in \Omega, \exists r \in \mathbb{R}_+^* | \mathcal{B}(a,r) \subset \Omega\)
Cette définition est plus qu’indigeste. Je vais essayer de l’expliquer élément par élément.
Déjà, attardons-nous sur \(\mathcal{B}(a,r)\), qui est la boule de centre \(a\) et de rayon \(r\). Par définition, on a \(\mathcal{B}(a,r)= \{ x \in \mathbb{R}^n | \|x-a \|< r \}\). Cela ne nous éclaire pas beaucoup.
Pour comprendre cette écriture, il faut s’interroger sur la raison qui a poussé les mathématiciens à appeler ces objets « boules » de \(\mathbb{R}^n\). En fait, c’est parce que la norme désigne une distance. Ainsi, si on devait décrire littéralement cet objet, on dirait que c’est « l’ensemble des vecteurs se situant à une distance de \(a\) inférieure à \(r\) ». Et on appelle donc cet objet une boule.
Donc, si on souhaitait dessiner une boule dans \(\mathbb{R}^2\), il s’agirait d’un disque, dans \(\mathbb{R}^3\), il s’agirait d’une boule.
Revenons à la définition
On dit qu’un ensemble est ouvert si en tout point de cet ensemble, il existe une boule de centre ce point incluse dans l’ensemble. Si on souhaitait vulgariser la notion d’ouvert, on dirait que c’est un objet que l’on ne peut pas dessiner, car il n’a pas de « frontière ».
En effet, imaginons que je dessine une forme quelconque, disons une ellipse, sur une feuille de papier. Il s’agit d’une partie de \(\mathbb{R}^2\). Considérons un point situé sur le bord de l’ellipse. Il y a des points dans l’entourage de ce point (donc, dans une boule de centre ce point) qui ne seront pas à l’intérieur de l’ellipse. Cette forme n’est donc pas un ouvert d’après la définition.
En revanche, si je retire la ligne qui dessine la frontière de cette forme, j’obtiens un ouvert.
En vulgarisant à l’extrême, on peut donc dire qu’un ouvert est une partie qui n’a pas de frontière.
Un fermé de \(\mathbb{R}^n\)
À notre niveau, le cours est relativement simple sur la notion de fermé. On dit qu’un ensemble est fermé lorsqu’il est le complémentaire d’un ouvert.
En vulgarisant à l’extrême, on peut dire qu’un fermé est une partie qui a une frontière.
Quelques propriétés
On a au total sept propriétés sur les ouverts et les fermés dans le cours.
- \(\mathbb{R}^n\) et l’ensemble vide sont à la fois des ouverts et des fermés.
- Une union dénombrable d’ouverts est un ouvert.
- Une intersection finie d’ouverts est un ouvert.
- Une intersection dénombrable de fermés est un fermé.
- Une union finie de fermés est un fermé.
- Soit \(\Omega\) une partie de \(\mathbb{R}^n\), \(f\) une fonction continue sur \(\Omega\), et \(a\) un réel quelconque. Les ensembles \(\{x \in \Omega | f(x) \ge a \} \)et \(\{x \in \Omega | f(x) \le a\}\) sont des fermés.
- Les ensembles \(\{x \in \Omega | f(x) > a \} \)et \(\{x \in \Omega | f(x) < a\}\) sont des ouverts.
Dans les faits, si on te demande de démontrer qu’un ensemble est un fermé ou un ouvert, cela sera souvent en utilisant une ou plusieurs de ces propriétés que tu t’en sortiras.
Il arrive, dans des cas très rares, de devoir passer à la définition pour montrer qu’un ensemble est un ouvert ou un fermé. C’est alors de loin la question la plus difficile du sujet. Je te recommanderais donc d’admettre immédiatement toute question sur les ouverts et les fermés qui ne se résoudrait pas en utilisant ces propriétés.
Mais si tu souhaites tout de même voir à quoi ressemble une réponse à ce genre de question, regarde la correction de la question 13)a) de HEC 2010 Maths 1 (à la page 23 de ce corrigé). L’énoncé du sujet est déjà au début de l’article.
Un borné de \(\mathbb{R}^n\)
On dit qu’une partie \(\Omega\) de \(\mathbb{R}^n\) est bornée lorsqu’il existe un réel positif \(r\) tel que
\(x \in \Omega \Rightarrow \|x\| \le r \)
Si tu as bien compris la définition des boules, tu peux donc remarquer que \(\Omega \) est bornée s’il existe un rayon \(r\) tel que \(\Omega \subset \mathcal{B}(0,r)\)
Pour démontrer qu’une partie de \(\mathbb{R}^n\) est bornée, il te suffira donc d’en prendre un élément quelconque, puis par une suite d’implications, de démontrer que sa norme est inférieure à un certain réel positif.
Les notions hors programme
Beaucoup d’éléments que j’ai cités précédemment pourraient déjà être considérés comme hors programme (en dehors des sept propriétés sur les ouverts et les fermés), bien qu’au cœur des résultats de l’optimisation. Il existe en revanche d’autres notions qui, elles, sont bien hors programme. Mais pas moins récurrentes lorsque l’on parle de topologie.
Les ensembles convexes
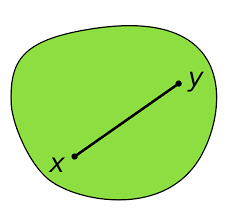
On dit qu’une partie \(\Omega\) de \(\mathbb{R}^n\) est convexe, lorsque \(\forall (x,y) \in \Omega^2, \forall \lambda \in [0,1], \lambda x + (1- \lambda) y \in \Omega\)
Pour comprendre cette définition, il faut d’abord comprendre que lorsque \(\lambda\) décrit le segment \([0,1]\), \(\lambda x + (1- \lambda) y\) décrit le segment (de \(\mathbb{R}^n\)) \(x\) \(y\), c’est-à-dire tous les vecteurs qui se situent sur la droite de \(\mathbb{R}^n\) passant par \(x\) et \(y\), entre \(x\) et \(y\).
Alors, une partie convexe est un ensemble tel que, quels que soient les points choisis dans cet ensemble, tous les points du segment qui les relie font partie de cet ensemble.
Si on vulgarise, on peut dire qu’un ensemble convexe est un ensemble dont le dessin n’a pas de renfoncement, ou de golfe, au sens géographique. Car s’il a un golfe, il suffit de prendre un point de chaque côté du golfe, et une grande partie du segment ne ferait pas partie de l’ensemble.

Conclusion
La topologie est donc un domaine très complexe, dès lors que l’on sort des sentiers battus. Ces quelques notions t’aideront, je l’espère, à te repérer.
N’hésite pas à consulter toutes nos ressources en mathématiques !