La notion de projecteur est majeure dans le programme d’algèbre linéaire et bilinéaire d’ECG en mathématiques approfondies. Cet article constitue un récapitulatif de ce que tu dois absolument connaître pour réussir le jour J. Tu vas y trouver les définitions à connaître par cœur, les propriétés fondamentales à savoir, ainsi que des graphiques pour mieux appréhender les projecteurs.
Attention, cet article s’adresse aussi bien aux maths appliquées qu’aux maths approfondies pour la partie « projecteurs ». En revanche, comme la théorie de l’algèbre bilinéaire n’est pas au programme des maths appliquées, les projecteurs orthogonaux s’adressent seulement aux maths approfondies.
La définition d’un projecteur en algèbre linéaire (mathématiques)
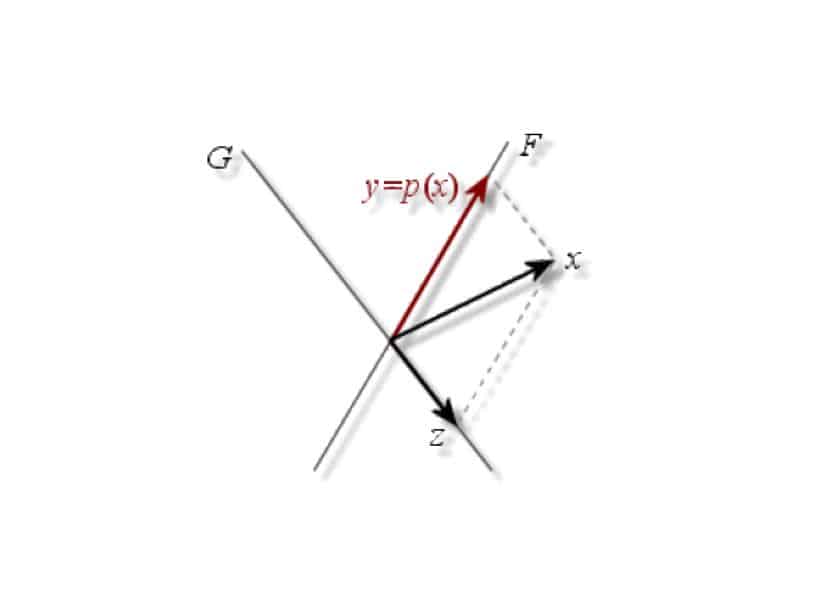
Soient \( E \) un \( \mathbb{R} \)-espace vectoriel quelconque, \( A \) et \( B \) deux sous-espaces vectoriels supplémentaires dans \( E \) (\( E = A \oplus B \)).
On dit que \( p \) est le projecteur de \( E \) sur \( A \) parallèlement à \( B \) si et seulement si : \[ \forall x \in E, \exists! (a_{x}, b_{x}) \in A \times B \ / \ x = a_{x} + b_{x} \Rightarrow p(x) = a_{x} \]
Comprendre la notion de projecteur géométriquement
Bien que les espaces vectoriels les plus souvent utilisés soient de dimension \( n \in \mathbb{N}^{*} \), il est avant tout indispensable de passer par des espaces vectoriels de dimension 2 ou 3 afin d’appréhender au mieux la notion de projecteur. Quoi de mieux que deux exemples, un dans \( \mathbb{R}^{2} \) et un dans \( \mathbb{R}^{3} \).
N.B. : Tu peux retrouver des schémas sur \( \mathbb{R} \) et sur \( \mathbb{R}^{2} \) qui t’expliquent le fonctionnement d’un simple vecteur dans ces ensembles via les notations \(\text{Vect}\) en cliquant ici.
Dans \( \mathbb{R}^{2} \)
Posons \( E = \mathbb{R}^{2}, \ A = \text{Vect}((1,0)), \ B = \text{Vect}((0,1)) \) et \( p \) le projecteur de \( E \) sur \( A \) parallèlement à \( B \) (on a bien \( E = A \oplus B \)). Ainsi, d’après la définition d’un projecteur, on a : \[ \forall (x,y) \in \mathbb{R}^{2}, \ p((x,y)) = (x,0) \]
Pour \( \color{blue}{u = (1,1)} \) et \( \color{red}{v = (-3,-1)} \), on a : \[ \color{green}{p(u) = (1,0)} \quad \text{et} \quad \color{magenta}{p(v) = (-3,0)} \]
Sur le graphique ci-dessous, tu peux apercevoir les vecteurs \( \color{blue}{u} \), \( \color{red}{v} \), \( \color{green}{p(u)} \) et \( \color{magenta}{p(v)} \) :
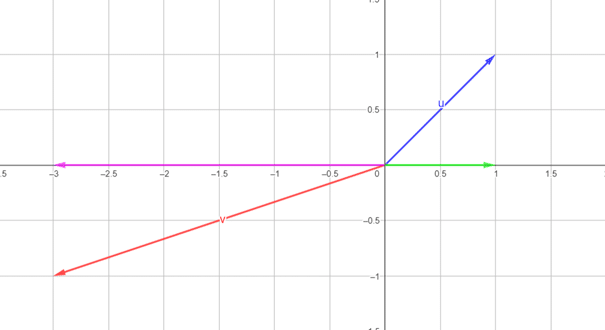
Je pense que tu commences à comprendre ce que fait un projecteur. Ici, le projecteur \( p \) projette tout vecteur sur la droite vectorielle \( \text{Vect}((1,0)) \), autrement dit l’axe des abscisses.
Plus généralement, tout projecteur de \( \mathbb{R}^{2} \) projette ses vecteurs sur une droite (à l’exception de l’application nulle et identité de \( \mathbb{R}^{2} \), notés respectivement \( 0_{\mathbb{R}^{2}} \) et \( \text{id}_{\mathbb{R}^{2}} \)).
Dans \( \mathbb{R}^{3} \)
Pour ce qui est de \( \mathbb{R}^{3} \), c’est un peu différent… Là où tous les projecteurs de \( \mathbb{R}^{2} \) projetaient sur une droite (sauf \( 0_{\mathbb{R}^{2}} \) et \( \text{id}_{\mathbb{R}^{2}} \)), les projecteurs de \( \mathbb{R}^{3} \), eux, projettent soit sur une droite (espace vectoriel engendré par un seul vecteur), soit sur un plan (espace vectoriel engendré par deux vecteurs).
Pourquoi ? En fait, tout dépend de la dimension sur laquelle les projecteurs de \( \mathbb{R}^{3} \) projettent… Considérons les deux exemples qui suivent.
Posons \( E = \mathbb{R}^{3}, \ A = \text{Vect}((1,0,0),(0,1,0)), \ B = \text{Vect}((0,0,1)) \) et \( p \) le projecteur de \( E \) sur \( A \) parallèlement à \( B \) et \( q \) le projecteur de \( E \) sur \( B \) parallèlement à \( A \) (on a bien \( E = A \oplus B \)). Ainsi, d’après la définition d’un projecteur, on a : \[ \forall (x,y,z) \in \mathbb{R}^{3}, \ p((x,y,z)) = (x,y,0) \]
Et : \[ \forall (x,y,z) \in \mathbb{R}^{3}, \ q((x,y,z)) = (0,0,z) \]
En étant assez attentif, on déduit que \( p \) projette sur un plan et \( q \) sur une droite.
Pour \( \color{blue}{u = (3,2,2)} \), on a : \[\color{red}{p(u) = (3,2,0)} \quad \text{et} \quad \color{green}{q(u) = (0,0,2)} \]
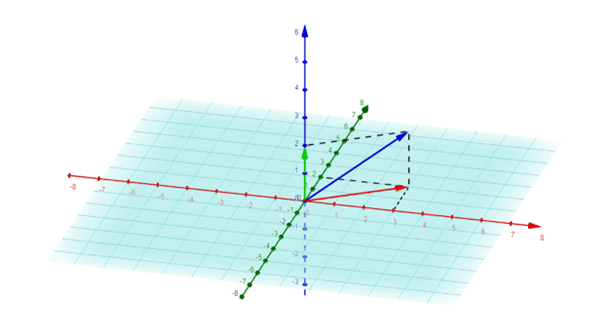
En suivant le code couleur, on reconnaît bien \( \color{blue}{u} \), \( \color{red}{p(u)} \), \( \color{green}{q(u)} \) ainsi que le plan \( \color{turquoise}{A} \).
Quelques propriétés fondamentales (à connaître par cœur)
Maintenant que tu as compris en quoi consiste un projecteur, voici une liste succincte des propriétés fondamentales sur les projecteurs que tu dois absolument connaître par cœur :
- Si \( p \in \mathcal{L}(E) \), on a : \[ \fbox{\( p \ \text{est un projecteur} \Leftrightarrow p \circ p = p \)} \]
Dans ce cas, \( E = \text{Im}(p) \oplus \text{ker}(p) \) et \( p \) est le projecteur de \( E \) sur \( \text{Im}(p) \) parallèlement à \( \text{ker}(p) \).
- On a : \[ \fbox{\( x \in \text{Im}(p) \Leftrightarrow p(x) = x \)} \]
- Pour \( p \) projecteur sur \( A \) parallèlement à \( B \), on a : \[ \fbox{\( \forall x \in E, \ x = a_{x} + b_{x}, \ \text{avec} \begin{cases} a_{x} = p(x) &\in A\\ b_{x} = x – p(x) &\in B \end{cases} \)} \]
Et on en déduit que : \[ \fbox{\( y = p(x) \Leftrightarrow y \in A \ \text{et} \ x – y \in B\)} \]
Remarque : \( \text{id}_{E} – p \) est le projecteur sur \( B \) parallèlement à \( A \). On a aussi \( A = \text{Im}(p) = \text{ker}(\text{id}_{E} – p) \) et \( B = \text{ker}(p) = \text{Im}(\text{id}_{E} – p) \)
- Soit \( C \) une base adaptée à \( E = A \oplus B \) (formée par concaténation d’une base de \( A \) et d’une base de \( B \)). Dans ce cas, puisque pour tout \( x \in A \) et \( y \in B \), \( p(x) = x \) et \( p(y) = 0 \), on a : \[ \fbox{\( \text{Mat}_{C}(p) = \begin{pmatrix} I_{r} & 0_{r,n-r} \\ 0_{n-r,r} & 0_{n-r}\end{pmatrix} \ \text{où} \ n = \dim(E) \ \text{et} \ r = \dim(A) \)} \]
- Soit p un projecteur dans \( \mathcal{L}(E) \). En notant \( \text{Tr}(p) \) la trace de la matrice de \( p \) dans n’importe quelle base de \( E \), on déduit du quatrième point que : \[ \fbox{\( \text{Tr}(p) = \text{rg}(p) \)} \]
Démonstration
Soient \( C_{1} \) une base adaptée à \( E = A \oplus B \) et \( C_{2} \) une base quelconque de \( E \). On note \( P \) la matrice de passage de la base de \( C_{2} \) à \( C_{1} \) et \( D \) la matrice \( \text{Mat}_{C_{1}}(p) \) (matrice diagonale telle que définie par le quatrième point). On a alors :
\[ \text{Mat}_{C_{2}}(p) = PDP^{-1} \quad (\star) \]
Or, pour toutes matrices \( U \) et \( V \) de \( \mathcal{M}_{n} (\mathbb{R}) \), on a :
\[ \text{Tr}(UV) = \text{Tr}(VU) \]
Ainsi, avec \( P \) et \( DP^{-1} \) en lieu et place de \( U \) et \( V \), on a :
\[ \begin{align}\text{Tr}(P(DP^{-1})) &= \text{Tr}((DP^{-1})P) \\ &= \text{Tr}(D) \qquad \qquad \text{car} \ P^{-1}P = \text{I}_{n} \end{align} \]
De \( (\star) \), on déduit que :
\[ \text{Tr}(\text{Mat}_{C_{2}}(p)) = \text{Tr}(D) \quad (\star \star) \]
Or, rappelons (d’après le quatrième point) que :
\[ \begin{align}D &= \text{Mat}_{C_{1}}(p) \\ &= \begin{pmatrix} I_{r} & 0_{r,n-r} \\ 0_{n-r,r} & 0_{n-r}\end{pmatrix} \ \text{où} \ n = \dim(E) \ \text{et} \ r = \dim(A) \end{align} \]
D’où :
\[ \begin{align}\text{Tr}(D) &= r \\ &= \dim(A) \\ &= \text{rg}(p) \qquad \text{car} \ \text{Im}(p) = A \ (\text{puisque} \ p \in \mathcal{L}(E)) \end{align} \]
De \( (\star \star) \), on déduit que :
\[ \text{Tr}(\text{Mat}_{C_{2}}(p)) = \text{rg}(p) \]
Puisque \( C_{2} \) est une base quelconque de \( E \), on a bien : \[ \text{Tr}(\text{Mat}_{C_{2}}(p)) = \text{Tr}(p) \]
Cela nous permet dès lors d’aboutir au résultat.
Le cas particulier des projecteurs orthogonaux (seulement maths approfondies)
Définition de projecteur orthogonal
Soient \( E \) un \( \mathbb{R} \)-espace vectoriel quelconque et \( F \) un sous-espace vectoriel de \( E \).
On dit que \( p \) est le projecteur orthogonal de \( E \) sur \( F \) lorsque \( p \) est le projecteur de \( E \) sur \( F \) parallèlement à \( F^\perp \).
Comment interpréter géométriquement la notion de projecteur orthogonal ?
En revenant à la définition d’orthogonal (« qui forme un angle droit »), on pourrait d’ores et déjà comprendre en quoi consiste un projecteur orthogonal. En fait, dans \( \mathbb{R}^{2} \) et dans \( \mathbb{R}^{3} \), un projecteur orthogonal projette tout vecteur sur une droite ou un plan de manière que le vecteur projeté forme un angle droit avec le vecteur initial. Pour mieux le comprendre, rien de mieux que des illustrations.
Reprenons les deux exemples de projecteurs vus précédemment dans \( \mathbb{R}^{2} \) et \( \mathbb{R}^{3} \) (que l’on note désormais \( p_{1}, p_{2} \) et \( p_{3} \). On pose également \( A = \text{Vect}((1,0)), \ B = \text{Vect}((0,1)), \ C = \text{Vect}((1,0,0),(0,1,0)) \) et \( D = \text{Vect}((0,0,1)) \).
On avait vu que : \[ \begin{cases} p_{1} \ \text{est le projecteur de} \ \mathbb{R}^{2} \ \text{sur} \ A \ \text{parallèlement à} \ B \\ p_{2} \ \text{est le projecteur de} \ \mathbb{R}^{3} \ \text{sur} \ C \ \text{parallèlement à} \ D \\ p_{3} \ \text{est le projecteur de} \ \mathbb{R}^{3} \ \text{sur} \ D \ \text{parallèlement à} \ C \end{cases} \]
Or, on remarque que : \[ \begin{cases} B = A^\perp \\ D = C^\perp \\ C = D^\perp \end{cases} \]
Donc : \[ \begin{cases} p_{1} \ \text{est le projecteur orthogonal de} \ \mathbb{R}^{2} \ \text{sur} \ A \\ p_{2} \ \text{est le projecteur orthogonal de} \ \mathbb{R}^{3} \ \text{sur} \ C \\ p_{3} \ \text{est le projecteur orthogonal de} \ \mathbb{R}^{3} \ \text{sur} \ D \end{cases} \]
Ces projecteurs étaient en réalité des projecteurs orthogonaux. Voici alors les mêmes graphiques que précédemment, mais avec les angles droits mis en évidence :
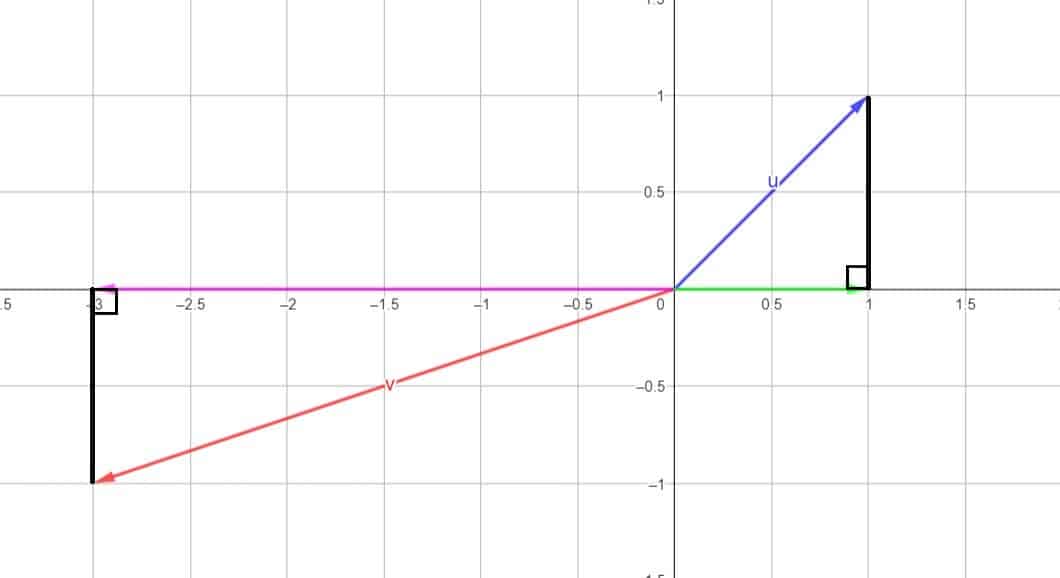
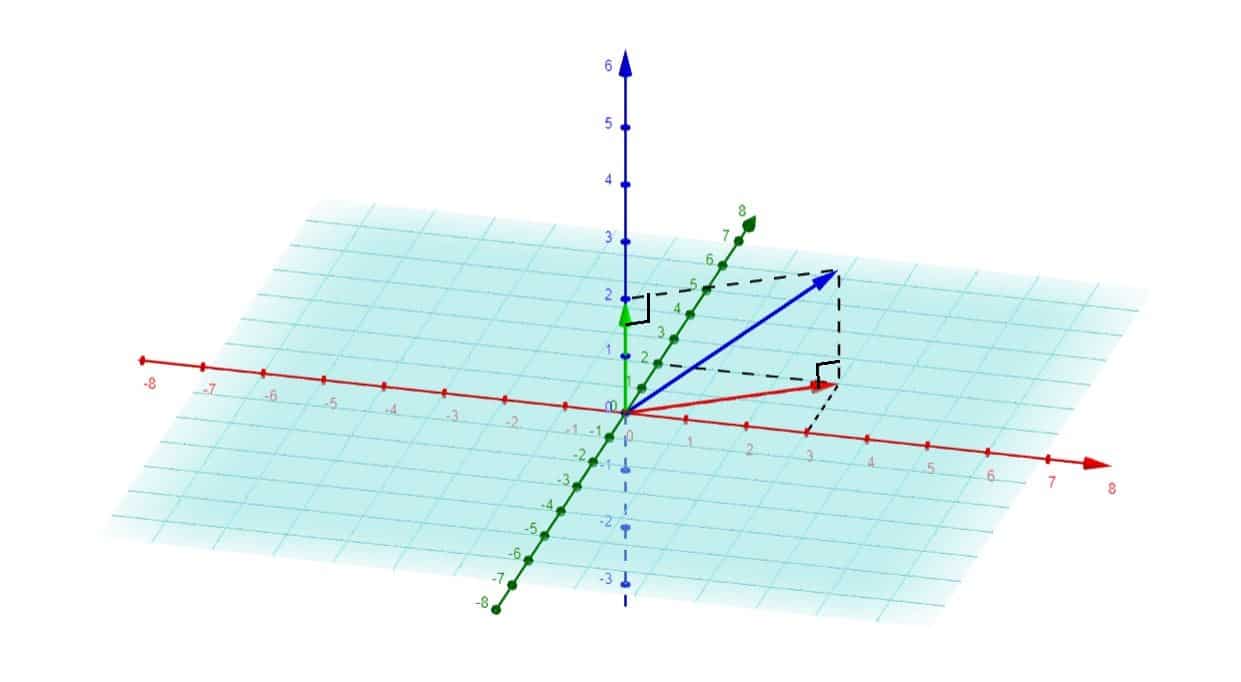
Dans le cas général, un projecteur orthogonal \( p \) projette tout vecteur \( u \) d’un espace vectoriel \( E \) sur un sous-vectoriel \( F \) de telle sorte que la distance entre le vecteur projeté \( p(u) \in F \) et le vecteur initial \( u \) (cette distance est égale à \( \|u-p(u)\| \)) soit minimale. En effet, dans \( \mathbb{R}^{2} \) et dans \( \mathbb{R}^{3} \), le seul et unique vecteur \( p(u) \) qui réalise cette distance minimale est le vecteur qui forme un angle droit avec le vecteur initial \( u \).
Les propriétés des projecteurs orthogonaux à savoir par cœur
Voici la liste des propriétés que tu dois apprendre pour gagner un maximum de temps le jour J (et faire la différence avec les autres candidats).
- On a : \[ \fbox{\( \small{p \ \text{est un projecteur orthogonal} \Leftrightarrow \text{Im}(p)^\perp = \text{ker}(p) \Leftrightarrow \text{ker}(p)^\perp = \text{Im}(p) \Leftrightarrow \text{Im}(p) \perp \text{ker}(p)} \)} \]
- Pour tout projecteur orthogonal \( p \) de \( E \), on a : \[ \fbox{\( y = p(x) \Leftrightarrow y \in F \ \text{et} \ x – y \in F^\perp \)} \]
- On en déduit que pour tout projecteur orthogonal \( p \) de \( E \) : \[ \fbox{\( \forall x \in E, \ \langle p(x),x-p(x)\rangle = 0 \)} \]
- Si \( B_{F} = (e_{1},…,e_{k}) \) est une base orthonormale de \( F \) (de dimension \( k \)), alors : \[ \fbox{\( p : \begin{cases} E \to E \\ x \mapsto \displaystyle \sum_{i=1}^{k}\langle x,e_{i}\rangle e_{i} \end{cases} \ \text{est le projecteur orthogonal sur} \ F \)} \]
- Théorème de meilleure approximation : soit \( p \) le projecteur orthogonal sur le sous-espace vectoriel \( F \) de \( E \) et \( x \in E \) un vecteur quelconque fixé. On a alors pour tout \( v \in F \) : \[ \fbox{\( v = p(x) \Leftrightarrow \min_{u \in F} \|x-v\| = \|x-u\| \)} \] Remarque : on retrouve bien ici la notion de distance minimale évoquée dans l’illustration
- Pour tout projecteur \( p \), on a : \[ \fbox{\( p \ \text{est un projecteur orthogonal} \Leftrightarrow p \ \text{est symétrique} \)} \]
Rappel : un endomorphisme \( f \) de \( E \) est dit symétrique lorsqu’il vérifie : \[ \forall (x,y) \in E^{2}, \ \langle x,f(y)\rangle = \langle f(x),y\rangle \]
N’hésite pas à consulter toutes nos autres ressources de mathématiques !