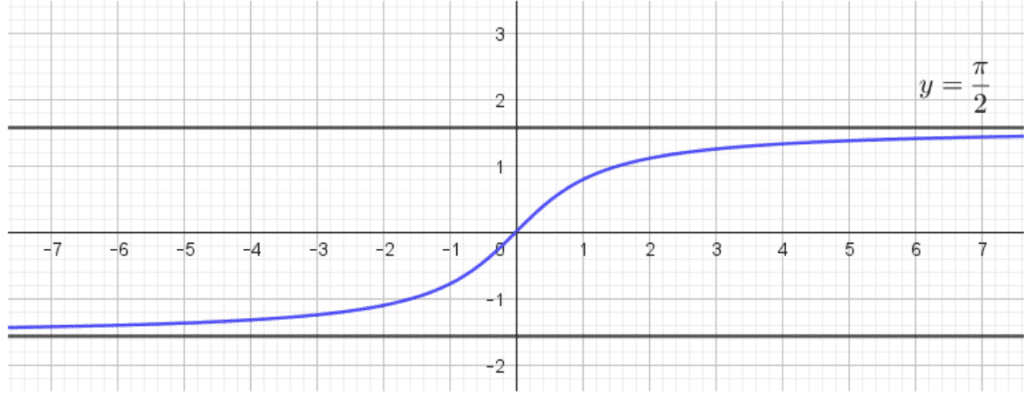
La fonction arctan tombe très fréquemment dans les sujets de concours. Étudions alors ses principales propriétés ! Les questions mises en avant dans cet article sont très classiques et les réponses sont à connaître sur le bout des doigts.
Petit zoom sur la fonction arctan
En mathématiques, l’arc tangente d’un nombre réel est la valeur d’un angle orienté dont la tangente vaut ce nombre. On rappelle que la fonction arctan :
- est la fonction réciproque de la restriction à l’intervalle ouvert \(\displaystyle]-\frac{\pi}{2},\frac{\pi}{2}[\) de la fonction \(tan\) ;
- est de classe \(C^{\infty}\) sur \(\mathbb{R}\) ;
- admet pour dérivée la fonction \(\displaystyle x \mapsto \frac{1}{1+x^{2}}\) pour tout \(x\) ∈ \(\mathbb{R}\) ;
- réalise une bijection de \(\mathbb{R}\) sur \(\displaystyle ]-\frac{\pi}{2},\frac{\pi}{2}[\) de la fonction \(tan\), c’est-à-dire que : \(y\) = \(\arctan(x)\) \(\Leftrightarrow\) \(\tan(y)\) = \(x\) et \(y\) \(\in\) \(\displaystyle ]-\frac{\pi}{2},\frac{\pi}{2}[\).
Pour finir, voici l’allure de sa courbe :
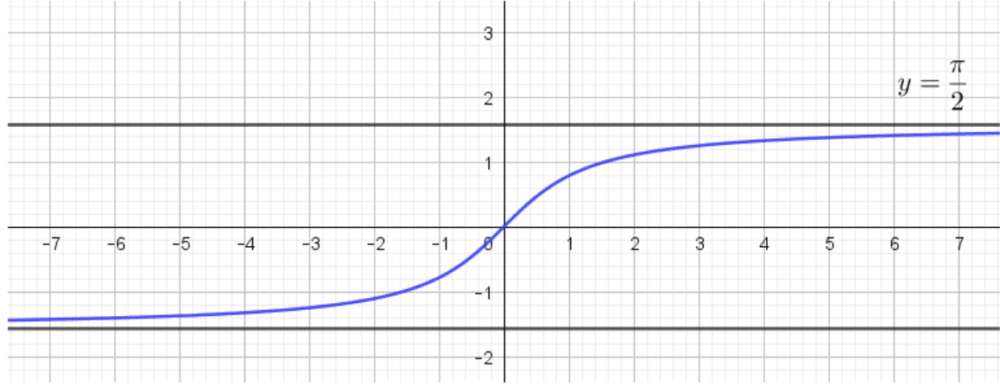
Quelques valeurs classiques à connaître
Les limites
Nous avons :
- \( \lim \limits_{x \to +\infty}\)\(\arctan(x)\)=\(\displaystyle\frac{\pi}{2}\)
- \(\displaystyle \lim \limits_{x \to -\infty}\)\(\arctan(x)\)=\(\displaystyle -\frac{\pi}{2}\)
Les asymptotes
La fonction possède deux asymptotes horizontales :
- \( \displaystyle y = -\frac{\pi}{2} \; \text{en} \; -\infty \)
- \(\displaystyle y = \frac{\pi}{2} \; \text{en} \; \infty \)
Les valeurs
- \(\arctan(0)\)=0
- \(\displaystyle \arctan(1)\)=\(\frac{\pi}{4}\)
L’imparité de la fonction arctan
La fonction \(arctan\) est impaire, c’est-à-dire que pour tout \(x ∈ \mathbb{R}, \arctan(-x)=-\arctan(x)\).
Démonstration
Parfois, comme dans ESSEC 2013 maths approfondies, un sujet pourrait te demander de justifier que la fonction \(arctan\) est impaire. Voyons alors la démonstration :
- Si la question est située dans un sujet de Parisiennes ou dans un oral, tu peux simplement répondre que la bijection réciproque d’une fonction impaire (qu’est la fonction \(\tan\)) est impaire.
- Si l’énoncé semble attendre une preuve, il faut alors redémontrer ce résultat de cours :
l’ensemble de définition de la fonction \(arctan\) est \(\mathbb{R}\), ensemble qui est bien centré en zéro.
De plus, \(\forall\) \(x\) ∈ \(\mathbb{R}\) et \(y = arctan(x)\). On a alors \(\tan(x)\) = \(y\) avec \(y\) ∈ \(\displaystyle ]-\frac{\pi}{2},\frac{\pi}{2}[\) . La fonction tangente étant impaire, on a finalement : \(\tan(-y)\) = \(-\tan(y)\) = \(-x\), d’où \(arctan(-x)\) = \(-y\) = \(-arctan(x)\). On en conclut que la fonction \(arctan\) est impaire.
Développement limité et équivalent
Tu seras sûrement amené(e) à calculer le développement limité de la fonction \(arctan\) (au maximum à l’ordre 3), ou bien à lui trouver un équivalent. Voici donc les démonstrations.
Développement limité à l’ordre 3 au voisinage de zéro
Justifions tout d’abord que ce développement limité existe. La fonction \(arctan\) est de classe \(C^3\), puisque sa dérivée est \(C^2\). Donc, par la formule de Taylor-Young, elle admet un développement limité à l’ordre 3 au voisinage de zéro.
Or, on a :
- \(\displaystyle \arctan'(x)\)=\(\displaystyle \frac{1}{1+x^{2}}\)
- \(\displaystyle \arctan^{(2)}(x)\)=\(\displaystyle -\frac{2x}{(1+x^{2})^{2}}\)
- \(\displaystyle \arctan^{(3)}(x)\)=\(\displaystyle \frac{-2(1+x^{2})^{2}+8x(1+x^{2})}{(1+x^{2})^{2}}\)
Et donc, le développement limité d’ordre 3 de \(arctan\) au voisinage de zéro est :
\(
\begin{align}
\arctan(x)&= \displaystyle \arctan(0)+\arctan'(0)x+\arctan^{(2)}(0)\frac{x^{2}}{2}+\arctan^{(3)}(0)\frac{x^{3}}{3!}+o(x^{3})\\
&= \displaystyle x-\frac{2}{6}x^{3}+o (x^{3})\\
\end{align}\)
D’où :
\[ \fbox{\( \displaystyle arctan(x)=x-\frac{2}{6}x^{3}+o (x^{3})\)}\]
Équivalent en zéro
On déduit du développement limité que \(\arctan(x)\underset{{0}}{\sim}x\).
Encadrement classique
Montrons que \(0 \le arctan(x) \le x ,\forall x ∈ \mathbb{R}^{+}\)
Méthode 1
La dérivée de \(arctan\) est négative sur \(\mathbb{R}^{+}\), donc \(arctan\) est concave sur \(\mathbb{R}^{+}\). Elle est donc située en dessous de ses tangentes. Or, la tangente de \(arctan(x)\) en 0 est la droite d’équation \(y=x\), et donc \(\forall x ∈ \mathbb{R}^{+}, \arctan(x)≤x\).
D’autre part, \(arctan\) est croissante sur \(\mathbb{R}\) et \(arctan(0)=0\), donc \(\forall x ∈ \mathbb{R}^{+}, 0≤\arctan(x)\).
Méthode 2
\(\forall t ∈ \mathbb{R}^{+},0 \le \displaystyle \frac{1}{1+t^{2}} \le 1\)
Donc, par croissance de l’intégrale :
\( \displaystyle \forall x \in \mathbb{R}^{+}\), on a \(0 \le \displaystyle \int_{0}^{x}\frac{1}{1+t^{2}} \,
\mathrm{d}t \le \displaystyle \int_{0}^{x} 1\) =\(x\)
D’où : \(0 \le \arctan(x)-\arctan(0)\le x \Leftrightarrow 0 \le \arctan(x)\le x\)
Montrons que \(\forall x ∈ \mathbb{R}, |\arctan(x)|≤ \displaystyle \frac{1}{1+x^{2}}\)
On sait que :
- \(arctan'(x)\)=\(\displaystyle \frac{1}{1+x^{2}}\)
- \(arctan^{(2)}(x)\)=\( \displaystyle -\frac{2|x|}{(1+x^{2})^{2}}\)
Donc, \(|arctan^{(2)}(x)|\)=\(\displaystyle \frac{2|x|}{(1+|x|^{2})^{2}}\)
Or, \(\forall x ∈ \mathbb{R}, (1-x)^2 ≥ 0 \Leftrightarrow 1-2x+x^{2} ≥ 0 \Leftrightarrow 2x ≤ 1+x^{2}\)
En particulier, on a \(2|x|≤ 1+|x|^{2}\), donc, en divisant par \(1+|x|^{2}\), on a \( 0 \le \displaystyle \frac{2|x|}{(1+|x|^{2})^{2}}\le 1\)
Finalement, en multipliant les membres de l’inégalité par \(1+x^{2}\), on a \(|arctan^{\prime \prime}(x)|≤ \displaystyle \frac{1}{1+x^{2}}\)
Égalité classique
Montrons que \(\forall x ∈ \mathbb{R}_{+}^{*},\arctan(x)+\arctan(\frac{1}{x})=\frac{\pi}{2}\)
Soit \(g\) la fonction définie sur \(\mathbb{R}_{+}^{*}\) par \(g(x)=\arctan(x)+\arctan(\frac{1}{x})\). Alors \(g\) est dérivable sur \(\mathbb{R}_{+}^{*}\) par somme de fonctions dérivables, et on a :
\(\forall x ∈ \mathbb{R}_{+}^{*}, g'(x)= \displaystyle \frac{1}{1+x^{2}}-\frac{1}{x^{2}}\frac{1}{1+\frac{1}{x^{2}}}= \frac{1}{1+x^{2}}-\frac{1}{1+x^{2}}=0\)
Donc, \(g\) est constante sur \(\mathbb{R}_{+}^{*}\).
Or, nous avons \(\displaystyle g(1)=2\arctan(1)=2\frac{\pi}{4}=\frac{\pi}{2}\)
Finalement, \(\forall x ∈ \mathbb{R}_{+}^{*}, g(x)=g(1)=\frac{\pi}{2}\) et on a \(\displaystyle \arctan(x)+\arctan(\frac{1}{x})=\frac{\pi}{2}\)
À noter : de la même manière, \(\forall x ∈ \mathbb{R}_{-}^{*}, \arctan(x)+\arctan( \displaystyle \frac{1}{x})=\displaystyle -\frac{\pi}{2}\)
J’espère que cet article t’aura été utile. Tu maîtrises maintenant la fonction \(\arctan\) sur le bout des doigts !
La trigonométrie expliquée dans une vidéo très complète
Si des paroles sont mieux que des mots pour ta compréhension de la trigonométrie, on t’invite à aller voir cette merveilleuse vidéo explicative de Ambroise réalisée sur notre chaîne youtube, il détaille vraiment tout sur tout de la trigonométrie dans les moindres détails…
Les sujets en rapport avec les formules de trigonométrie
Avec ça tu pourras performer au concours sur les formules de trigo. Je te conseille de faire aussi des annales à fond :
Et il y a encore bien d’autres annales traitant de ces formules de trigo.
Aller plus loin
Les fonctions de trigonométries peuvent être approfondies sous différentes formes. En effet, les fonctions sinus et cosinus ont donné lieu à de nombreuses notions hors programme (qui se trouvent régulièrement dans les sujets). Parmi elles, tu peux retrouver : voici un tableau récapitulatif de toutes nos ressources de trigonométrie sur Major Prépa, que ce soit aussi bien en termes de notions de cours comme de notions hors programme :
| Contenu de trigonométrie au programme et hors programme ECG | |
| Trigo au programme | Trigo hors programme |
| Tout sur les fonctions de trigonométrie cos et sin | Les fonctions de trigonométrie cosh et sinh (cosinus hyperbolique et sinus hyperbolique) |
| Fiche récapitulative des formules de trigo | Trigonométrie et nombres complexes |
| Démonstrations des formules trigonométriques | La loi arcsinus standard et à support borné |
| Zoom sur la fonction Arctangente (Arctan et toutes ses méthodes associées) | Les intégrales de Wallis |
| Vidéo explicative de la trigonométrie | L’intégrale de Dirichelet |
| La trigonométrie (du point de vue du lycée, trigo troisième, trigonométrie en seconde…) | Transformée de Fourier (mais il y a des nombres complexes…) |
| Tout comprendre sur le cercle trigonométrique | |
N’hésite pas à consulter toutes nos ressources mathématiques !