Hello! Aujourd’hui, nous allons nous intéresser à une technique classique d’approximation : la méthode des rectangles. Cette méthode a longtemps été vue en classe, mais est maintenant hors programme. Elle reste très intéressante à explorer et te permet de travailler sur les intégrales. En bonus, on fait même un peu de programmation.
Présentation
Pour rappel, calculer une intégrale revient grosso modo à calculer l’aire sous la courbe.
Le problème, c’est que cette surface a une forme très particulière. Tu ne connais donc pas de formule pour trouver facilement cette aire.
On peut essayer de remplacer cette surface par des rectangles. Leurs aires sont bien plus simples à calculer ! Il suffit de les sommer pour avoir une estimation de l’aire sous la courbe et donc de la valeur de l’intégrale.
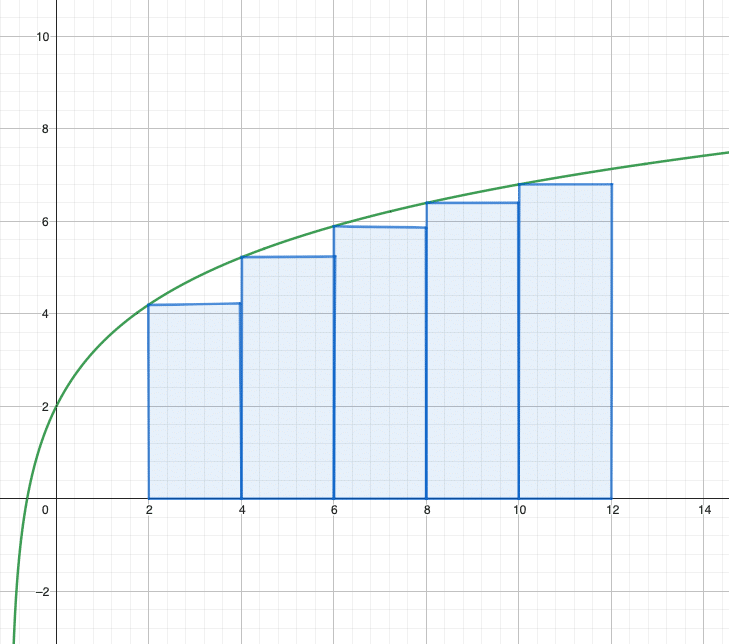
On peut faire l’approximation par en dessous ou par au-dessus.

C’est ce qu’on appelle la méthode des rectangles.
Explication
Soit \(n \in \mathbb N^*\).
On considère une fonction \(f\) continue sur un segment \([a,b]\). On coupe ce segment en \(n\) avec \(n \in \mathbb{N}\). Et on obtient donc \(n\) petits segments qui constituent la base de nos rectangles.
Pour \(k \in [\![0,n-1]\!]\), on note \(x_k=a+\frac{b-a}{n}k\).
D’un côté, on considère les rectangles « d’en dessous », qu’on note \(I_k\). Ils ont pour base \([x_k,x_{k+1}]\) et pour hauteur \(f(k)\).
De l’autre, on considère les rectangles « d’au-dessus », qu’on note \(S_k\). Ils ont pour base \([x_k,x_{k+1}]\) et pour hauteur \(f(k+1)\).
Si \(f\) est croissante sur \([a,b]\), on a par ailleurs \(\displaystyle \sum_{k=0}^{n}I_k \leq \displaystyle \int_{a}^{b} f(t) \,\mathrm{d}t \leq \displaystyle \sum_{k=0}^{n}S_k\). Bien évidemment, si \(f\) est décroissante sur \([a,b]\), on a \(\displaystyle \sum_{k=0}^{n}S_k \leq \displaystyle \int_{a}^{b} f(t) \,\mathrm{d}t \leq \displaystyle \sum_{k=0}^{n}I_k\).
Il apparaît intuitivement que plus \(n\) est grand, plus l’approximation sera précise. Par passage à la limite, on a donc la valeur de \(\displaystyle \int_{a}^{b} f(t) \,\mathrm{d}t\).
Un peu de Python
Voici un algorithme te donnant les valeurs de \(\displaystyle \sum_{k=0}^{n}I_k\) et de \(\displaystyle \sum_{k=0}^{n}S_k\).

Concrètement :
- on commence par définir la longueur de la base des rectangles ;
- ensuite, on ajoute à aire_inf et aire_sup, l’aire d’un nouveau rectangle ;
- on répète l’opération n fois grâce à la boucle for ;
- on définit par ailleurs la fonction \(f\) (ici, j’ai juste mis \(f(x)=3x^2+2\), désolée pour le manque d’originalité…) ;
- on exécute la fonction en choisissant les valeurs de \(a\), \(b\) et \(n\) (ici \(a=0\), \(b=1\) et \(n=100\)) ;
- on affiche enfin les deux valeurs obtenues.
Et voilà ! En augmentant la valeur de n, aire_inf et aire_sup vont se rapprocher jusqu’à te donner la valeur de l’intégrale.
Méthode des trapèzes
On procède de la même façon. Cette fois, cependant, on fait une approximation avec des trapèzes. Leurs formes épousent mieux la courbe ; l’estimation sera donc plus précise.

Quelques annales pour approfondir le thème
Plusieurs sujets s’appuient sur cette méthode sans le dire explicitement. Tu peux les regarder, c’est intéressant. En voici une liste non exhaustive :
- Exercice 1 Ecricome ECS 2016
- Exercice 2 Ecricome ECS 2008
- EDHEC ECS 2018 (Exercice 1, sujet 2)
Tu retrouveras même ce principe dans le sujet d’ECS HEC 2005.
J’espère que cet article t’a intéressé·e. N’hésite pas à aller jeter un œil à toutes nos autres ressources en mathématiques en cliquant juste ici.










