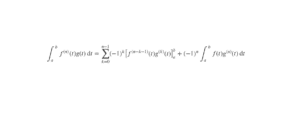L’épreuve de maths EDHEC ECE se déroule cette année le 4 juillet. Les concours ont été pertubés cette année, et Major-Prépa se mobilise pour te donner le plus vite possible les infos concernant les épreuves !
Tu peux retrouver ici le sujet de maths EDHEC ECE 2020 !
L’analyse sera publiée au plus vite !
Toutes les infos sur le concours 2020: Inside Concours BCE 2020
Analyse du sujet
L’épreuve EDHEC fermait la marche pour les mathématiques en cette année si particulière.
Le sujet respectait le découpage classique de cette épreuve, 3 exercices et un problème, pour balayer le plus largement possible l’ensemble du programme.
Exercice 1
Le sujet commençait par un sujet d’algèbre de facture assez classique, qui s’intéressait cette fois aux matrices antisymétriques.
La question 1. est une application directe du cours pour montrer qu’un sous-ensemble est un sous-espace vectoriel d’un espace de référence, à savoir l’ensemble des matrices carrées d’ordre n. Il est certainement primordial de rédiger parfaitement et efficacement cette question pour prendre un bon départ.
La question 2.a) demandait de bien connaître les propriétés opératoires avec les matrices, en particulier avec la transposition matricielle (attention au piège avec la transposée d’un produit).
La question 2.b) complétait 2.a) : pour montrer que f est un endomorphisme de M_n(|R), il ne restait plus qu’à prouver que c’est une application linéaire (et interpréter quand même le résultat précédent).
Après ces résultats généraux, on étudiait f dans un cas particulier où A était une matrice carrée d’ordre 3 donnée.
La question 3.a) est originale, pour faire assez « naturellement » faire apparaître (J,K,L) comme une famille génératrice de A_3(|R) il fallait partir de la forme explicite des matrices antisymétriques d’ordre 3 (en traduisant en termes de coefficients l’égalité tM = M si ne s’en souvenait plus).
Avec le théorème de la dimension, la question 3.b) tombait toute seule ensuite.
La question 4.a) demandait des calculs d’images, qui se ramenaient à des calculs de produits et sommes matriciels. Le plus important dans ce cas, est d’éviter les erreurs de calculs (qui sont basiques mais longs) et surtout de bien se souvenir que le but est d’écrire ces trois images comme combinaison linéaire des trois vecteurs de base J,K,L.
La question 4.b) était la suite logique, avec la propriété Im(f) = Vect((f(J),f(K),f(L)) qui donne directement une famille génératrice de Im(f)$, dont il reste à savoir si elle est libre ou pas.
La question 4.c) faisait ensuite assez logiquement intervenir le théorème du rang : on déduit dim Ker(f), et comme celle-ci vaut 1 il suffit de trouver une matrice non nulle qui appartient à ce noyau pour en être une base : cela tombe bien, K est un excellent candidat !
La question 5.a) réutilise à nouveau les calculs de 4.a) pour construire la matrice de f dans la base (J,K,L) fournie par l’énoncé. L’indication bienvenue à la fin (vérifier que tous les coefficients valent 0 ou -1) permettait de détecter une erreur de calcul éventuelle faite auparavant : vue l’importance des calculs d’images, il fallait alors prendre le temps de les reprendre s’il y avait un problème !
La forme triangulaire (inférieure) de la matrice F rendait immédiate la détermination des valeurs propres à la question 5.b), il fallait seulement bien citer la propriété.
La question 5.c) concluait de façon plus originale et aussi plus rapide, en passant une fois de plus par le théorème du rang pour trouver la dimension du deuxième sous-espace propre associé à la valeur propre -1 ( le premier étant Ker(f) = E_0(f)).
En conclusion, un exercice d’algèbre sans piège mais à la formulation ramassée pour lequel le travail sur les annales de l’Edhec permettait une bonne préparation.
C’est peu de dire que les amateurs d’algèbre linéaire auront été assez frustrés cette année avec leur absence totale aux sujets parisiens : un exercice comme celui-ci leur aura permis de rentrer rapidement dans le vif du sujet !
Exercice 2
Exercice consacré aux variables à densité, là aussi très ramassé, qui part d’une loi normale centrée (mais pas réduite), pour construire une nouvelle variable aléatoire qui permettra d’obtenir un estimateur de l’écart-type de la loi normale.
La question 1. est une question de cours qui redonne une propriété fondamentale de la loi normale centrée (vérifiée en fait, par n’importe quelle variable aléatoire admettant une densité paire), généralement abordée en fin de ECE1 qui possède une justification efficace à l’aide de propriétés d’intégrales de fonctions paires. On ne peut pas inventer la preuve, qu’il faut avoir étudiée et comprise.
Dans la question 2 on définit la variable aléatoire $Y = |X| qui est donc de fait une variable aléatoire positive.
En remarquant ce fait, à la question 2.a) on obtenait facilement en une phrase, la valeur de F_Y(x) pour x négatif. Le calcul pour x positif demande un travail soigneux avec la valeur absolue et les inégalités.
La question 2.b) est avant tout rédactionnelle : il faut soigneusement expliquer pouquoi F_Y est bien continue sur tout |R, de classe C1 sur |R sauf peut-être en un nombre fini de points. Le calcul de la densité f_Y se fait alors par dérivation de F_Y, sans piège ici (on réutilise alors la fonction f_X connue explicitement).
La question 2.c) est un calcul classique d’espérance, qui doit commencer par une justification soigneuse de l’absolue convergence de l’intégrale impropre qui définit E(Y) (souvent un peu rapidement traitée par les candidats, ce que déplore encore souvent le jury). Le but ici est d’avancer efficacement, sans sacrifier la rigueur pour prendre tous les points.
La question 3. concerne le chapitre d’estimation du programme : on travaille classiquement avec la moyenne empirique pour estimer l’espérance de Y, qui permettra celle du paramètre sigma.
La question 3.a) demande de savoir utiliser à bon escient la linéarité de l’espérance pour corriger le biais de l’estimateur S_n, afin d’en déduire un estimateur sans biais T_n. Pas de calcul compliqué mais il faut ici bien maîtriser le vocabulaire du chapitre d’estimation.
Question 3.b) : l’énoncé demande de rappeler la valeur du moment d’ordre 2 de X : c’est le moment de citer la formule de Koenig-Huygens, et d’exploiter le fait que cette fois c’est la variance qui donne E(X²), et par le contraire.
On en déduisait E(Y²) en remarquant que Y² = |X|² = X², il n’y avait donc plus aucun calcul d’intégrale à faire ici.
La question 4.c) concluait sur la convergence de l’estimateur sans biais T_n construit plus haut : la encore, il faut maîtriser les calculs classiques, savoir ce que vaut le risque quand le biais est nul notamment…
On finit par une simulation bien classique de la variable Y et donc de S_n pour finir par T_n : c’est très rapide à faire, cela rapporte un maximum de points, il est inenvisageable de ne pas remplir ces 4 trous à la fin d’un exercice ramassé à nouveau, original là encore dans sa formulation sans être totalement inédit.
Exercice 3
Un exercice consacré aux probabilités discrètes, auxquelles l’Edhec réserve traditionnellement – et c’est d’autant plus heureux cette année qu’on les aura vainement cherchées à Ecricome et à l’EMLyon, une place de choix, sur des énoncés là encore assez ramassés ces trois dernières années.
Il s’agit d’une expérience « à double détente », avec une première expérience qui détermine les conditions dans lesquelles se passe la suivante.
La question 1 « est très vite répondue » comme dirait l’autre ( !) si on interprète directement la conséquence du fait que n=1 : on fait forcément un seul tirage dans la deuxième urne, Y suit donc une loi de Bernoulli de paramètre p.
La question 2) est sans surprise et doit permettre aux candidats sérieux de montrer qu’ils se sont entraînés à justifier aussi rapidement qu’ils l’ont reconnue, la loi très simple de X, et à donner tout aussi vite son espérance et sa variance qui sont des résultats de cours.
La question 3) fait aussi intervenir une loi usuelle, mais vue cette fois comme loi conditionnelle : l’indication de l’énoncé selon laquelle il fallait bien distinguer les cas 0 <= i <= k et i>k n’est pas anodine !
Question 4) : on nous redonne gentiment les fonction Scilab qui simulent les lois usuelles discrètes ; mais pour le coup on nous en donne trop exprès, pour ne pas non plus nous donner la réponse ! la définition de Y utilise la valeur de X calculée juste au-dessus, c’est un grand classique qui là encore présente un ratio temps passé/points gagnés sans équivalent !
La question 5.a) demande une rédaction soigneuse, et pour le coup il fallait faire preuve d’initiative en pensant tout seul que le résultat de la question 3) appliqué au cas i=0 ne donnait que des probabilités conditionnelles pour [Y=0] : la formule des probabilités totales, la plus importantes de toutes les formules de probabilités discrètes, faisait ici son apparition !
La question 3.b) utilisait ici la même formule, sauf qu’il fallait faire bien attention aux indices (souvenez-vous de la distinction à la question 3) pour le cas général où on ne cherchait pas à calculer explicitement la somme obtenue (dont le nombre de termes était opportunément donné par l’énoncé, encore à des fins de vérification).
La question 6.a) demandait de redémontrer le résultat de cours dit « de la formule sans nom » : faire simple (calcul avec des factorielles) et efficace !
Synthèse de ce qui précède, la question 6.b) faisait apparaître une grosse formule sommatoire dans laquelle chacun doit trouver sa place.
Le but ultime est l’obtention en 6.c) d’un résultat miraculeusement simple après une formule du binôme de Newton et une somme de Gauss à repérer !
La question 7.a) voit le retour des grosses formules, avec le théorème de transfert et une loi toujours pas connue explicitement.
Même schéma de calcul ensuite pour 7.b) qu’en 6.b), sauf qu’il fallait bien utiliser deux fois à cette occasion, la formule sans nom. Les calculs de sommes avec les coefficients binomiaux sont abordés dès la première année, mais on n’a souvent pas trop de deux années de prépa pour les comprendre et savoir les appliquer correctement !
Une petite question 7.c) cadeau (même 1 point sur 150, cela se prend !!) et la question 7.d) revient à une relation très, très classique que tout bon préparationnaire doit savoir retrouver.
Problème
Un énoncé consacré à l’analyse cette fois : suite d’intégrales, série harmonique alternée, on se sent en terrain familier et en même temps le mélange de ces deux thèmes peut parfois dérouter les candidats.
La longueur également peut inquiéter, mais elle est essentiellement dûe au fait que l’énoncé détaille énormément l’étude pour permette aux candidats de sauter une question et d’avancer sans être bloqué par un résultat qui leur manquerait.
La question 1 peut semble piégeuse, on peut se demander ce qu’on doit dire : il suffit de prouver que les fonctions intégrées sont bien définies et continues sur [0 ;1] !
Dans la question 2., I_0 se calcule en reconnaissant une formule de primitive classique (1/u² -> -1/u).
I_1 est plus délicat, surtout sans indication : une IPP puis un jeu d’écriture (x = 1+x-1), il faut avoir longuement pratiqué ces calculs en entraînement pour avoir les bons réflexes.
Mais l’énoncé ne nous laisse pas dans la panade pour autant : les petits malins qui ont bien écouté leur professeur et qui ont bien regardé quelques questions après, auront repéré que I_0 et I_1 sont en fait donnés dans le script Scilab de la question 3.c), stockés initialement dans les variable a et b !
La question 3.a) demande d’utiliser la linéarité de l’intégrale et une identité remarquable ( !)
La question 3.b) applique le résultat précédent au cas où n=0, pour exprimer I_2 en fonction de I_0 et I_1 ce qui permet son calcul avec les valeurs précédemment calculées (ou déduites !)
La question 3.c) permettait un calcul de proche en proche, grâce à la relation de 3.a) qui donne I_n+2 en fonction des deux intégrales précédentes. Il faut avoir bien étudié la programmation des suites récurrentes sur deux générations en Scilab pour bien comprendre comment se faisait le transfert de valeurs entre les deux variables a (l’avant-dernière intégrale calculée) et b ( la dernière intégrale calculée), de même pour le terme 1/(n+1) de la formule de récurrence, qui devait être réécrit 1/(k-1) avec le jeu des décalages d’indices (ce qui était loin d’être évident !)
La question 4.a) est un grand classique, utilisant à la fois la positivité et la croissance de l’intégrale (avec citation de toutes les hypothèses nécessaires : continuité sur [0 ;1] des fonctions concernées et bornes dans l’ordre croissant !), avec prise d’initiative pour faire apparaître le terme 1/(n+1) à droite, qui est en fait l’intégrale de x^n entre 0 et 1 : il fallait donc de soi-même, penser à justifier que sur [0 ;1], x^n/(1+x)² <= x^n..
La question 4.b) est cadeau, ne vaut pas grand-chose mais un petit quelque chose + un autre petit quelque chose… chaque point compte !
La question 5 demandait de pratiquer une IPP, gentiment indiquée par l’énoncé. Le gros dilemme consiste à chaque fois à savoir quoi choisir pour les deux rôles à attribuer ; un indice : I_n fait intervenir x^n, et J_(n-1) utilise donc x^(n-1)… une idée ?
Question 6.a) : J_0 est facile à calculer, J_n+J_{n+1) aussi si on a pensé une fois de plus à la linéarité de l’intégrale (plus facile ici qu’en 3.a) d’ailleurs).
La question 6.b) est alors cadeau.
La question 7) est un bis repetita de la 3.c), sauf qu’ici la formule de récurrence ne porte que sur une seule génération : qui peut le plus, peut le moins !
La question 8) fait alors passer d’une définition des intégrales J_n de proche en proche, à une formule sommatoire donnant directement J_n : une récurrence s’impose ici, qu’on s’applique à proprement rédiger.
La question 9.a) est facile à faire si on tient bien compte de l’indication de l’énoncé !
La question 9 .b) est plus délicate : on comprend assez vite qu’il faut prouver la convergence de la série en trouvant une limite finie aux sommes partielles, mais il faut proprement gérer le (-1)^n qui est un terme divergent… passage par une valeur absolue ou encadrement -1 <= (-1)^n <= 1, il faut maîtriser l’un des deux au moins pour aller au bout, sans perdre de vue l’objectif initial.
La valeur de la somme totale ln(2) pour la série harmonique alternée est alors réobtenue.
La question 9.c) va un cran plus loin avec une prise d’initiative issue de l’entraîntement : pour prouver que I_n ~1/(alpha*n), on peut prouver que n*J_n tend vers une limite finie alpha, c’est la même chose, et c’est bien cela que permet la question 5. Cela demande du recul sur la notion d’équivalent, et en deuxième partie de problème, pressé par le temps, ce n’est pas forcément évident…
La question 10.a) n’est pas dure en soi, mais on n’a pas trop l’habitude de travailler avec des équivalents utilisant (-1)^n…
Attention aux erreurs grossières à la question 10.b), si vous avez pensé à l’absolue convergence oubliez tout de suite cette idée ! (-1)^n/(2n) = -1/2 * (-1)^(n-1)/n, il s’agit donc ni plus ni moins à un facteur près, de la série sur laquelle on a conclu en 9.a) !
Le problème est que le théorème de comparaison des séries ne s’applique qu’à des séries à termes POSITIFS, et qu’on ne peut donc rien conclure ici puisque (-1)^n/2n change sans cesse de signe d’un terme au suivant. La question ouverte (Peut-on… ?) et l’utilisation par l’énoncé du terme « impasse » à la question suivante( !) sont autant de signaux d’alertes qui permettront au jury de repérer immédiatement les contrevenants.
La question 11.a) est plus délicate, mais un sujet si long pouvait se le permettre pour donner du grain à moudre aux plus rapides : on l’obtenait assez vite si on avait l’idée de réorganiser le membre de droite (c’était de doute façon le plus compliqué des deux membres) en utilisant la relation simple u_k+1 = u_k + (-1)^k/(k+1) issue de la définition sommatoire de u_k et u_k+1 et du cas particulier de la relation de Chasles où on ne sort que le dernier terme dans u_(k+1).
L’égalité suivante en question 11.b) s’en déduisait par sommation de la relation précédente : à gauche on devait sentir qu’il fallait simplement rajouter un symbole somme, à droite un télescopage nous tendait les bras et il fallait gérer proprement une somme géométrique de raison (-1).
Le recours aux limites des deux suites extraites (S_2n) et (S_2n+1) est un peu limite quant aux contours stricts du programme, mais on pouvait difficilement s’en passer pour trouver les deux limites demandées (dans lesquelles les puissances de (-1) étaient de fait connues explicitement).
On espère que vous avez étudié (en classe ou sur Major-Prépa !) des exercices dans lesquels on faisait appel à ces deux suites dont la réunion des termes (et pas la somme !) fait la suite complète, pour pouvoir conclure que si (S_2n) et (S_2n+1) convergent vers la même limite (en l’occurrence 1/2 – ln(2)) alors il en est de même de la suite complète (S_n).
La question 12. est la friandise de la fin : il fallait repérer que u_n (et donc u_j) pouvait s’écrire sous la forme d’une seule somme (la somme totale de 1 à +oo moins la somme de 1 à j est la somme de j+1 à +oo) pour trouver comment réécrire la somme totale de la série de terme général u_k sous la forme d’une double somme (spoiler alert : la bonne réponse est la c) ).
Conclusion
C’est un vrai bon sujet de l’Edhec en ce qu’il balaie énormément de notions du cours de ECE et a largement donné de quoi s’occuper pendant quatre heures… et plus ! A moins d’être un carré ou un cube surentraîné pour être capable de le finir en moins de trois heures, l’essentiel était d’avancer efficacement certes, mais en prenant le temps de soigner les justifications.
Comme toujours avec un sujet si long, le jury devra adapter le barème, ce qui ne sera pas forcément à l’avantage des plus forts : que vous ayez 20,5/30 ou 29/30, si on coupe à 20 les deux copies seront notées 20 !