Aujourd’hui, on va travailler ensemble sur une nouvelle loi classique (mais hors programme) de probabilité : la loi de Weibull. C’est l’occasion pour toi de revoir quelques méthodes avec les probabilités continues (variables aléatoires à densité). C’est parti !
Présentation de la loi de Weibull
La loi de Weibull permet de faire des approximations de distribution. Elle est très utilisée par les ingénieurs grâce à sa capacité à tenir compte de différents types de répartition.
Elle permet ainsi d’évaluer la fiabilité et la résistance des matériaux, ou encore de décrire n’importe quelle phase de la durée de vie d’un produit lorsque le taux de défaillance est fonction du temps (si ce n’est pas le cas, une loi exponentielle suffit). Pratique, non ?
Fonction de répartition
La loi de Weibull repose sur deux paramètres positifs : \(\alpha\) pour la forme et \(\lambda\) comme échelle de temps. La fonction de répartition est la suivante :
\(\forall x > 0, F(x)=1-e^{(-(\lambda x)^{\alpha})}\) et \(\forall x \le 0, F(x)=0\)
On peut vérifier la continuité en 0 de cette fonction, ce qui permet de garantir qu’il s’agit bien d’une fonction de répartition d’une variable à densité. Je te laisse chercher sa densité en dérivant.
Tu as bien trouvé que \(f(x)=\alpha \lambda e^{- (\lambda x)^{\alpha}} x^{\alpha -1}\) si \(x>0\) et 0 sinon ?
Espérance et variance
Une variable suivant la loi de Weibull admet une espérance. Il suffit de montrer que \(\int^{+\infty }_{-\infty}x.f\left(x\right)dx\) converge.
Encore une fois, faire les calculs toi-même est le meilleur des entraînements. Cela te permettra de revoir la fonction gamma et les changements de variables. Mais voici quand même le résultat :
\(E(X)=\int_0^{+\infty} x\times \frac{\alpha}{\lambda}\left(\frac{x}{\lambda}\right)^{\alpha-1}exp^{-\left(\frac{x}{\lambda}\right)^{\alpha}}dx\)
On pose \(u=\left(\frac{x}{\lambda}\right)^{\alpha}\)
Finalement, on a :
\(E(X)=\lambda\int_0^{+\infty}u^{\frac 1 k}\times e^{-u}du = \lambda \times \Gamma\left(1+\frac 1 k\right)\)
Pour rappel, la fonction gamma est définie sur \(\mathbb{R}_{+}^{*}\) par \(\forall x \in \mathbb R^*_+, \Gamma(x)=\int_0^{+\infty}t^{x-1}e^{-t}dt\) et on a \(\forall z \in \mathbb{R}_{+}^{*} , \Gamma(z+1)=z\Gamma(z)\)
Pour ce qui est de la variance, la démarche est similaire.
Risque de défaillance
À savoir que :
- si \(\alpha >1\)
Le taux de défaillance croît avec le temps. C’est le cas la plupart du temps.
- si \(\alpha =1\)
Tu reconnais une loi exponentielle.
- si \(\alpha <1\)
Ce cas est rare, cela signifie que la machine a davantage de risque de tomber en panne lors de sa mise en marche.
Le plus intéressant est de voir la représentation graphique de la densité pour voir quelle est l’influence de \(\alpha\) et \(\lambda\).
J’ai choisi de me concentrer sur le premier cas, qui est le plus classique. On choisit arbitrairement plusieurs valeurs. On a les courbes suivantes :
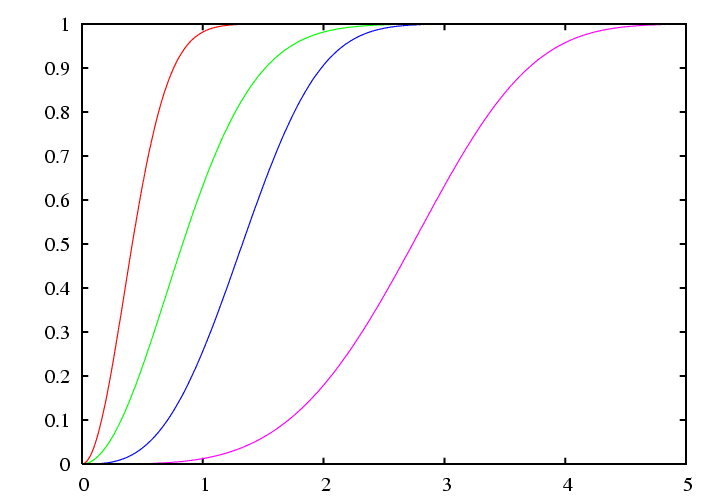
Fonction de répartition
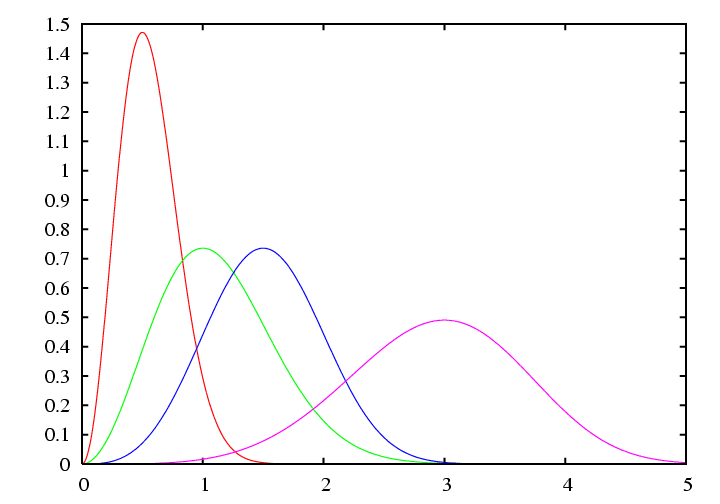
Densité
On a ici choisi pour la courbe rouge \(\lambda = \frac{1}{2}\) et \(\alpha=2\), pour la verte \(\lambda = 1\) et \(\alpha=2\), pour la bleue \(\lambda = \frac{3}{2}\) et \(\alpha=3\) et enfin pour la rose \(\lambda = 3\) et \(\alpha=4\)
Et pour info, si \(\alpha = 2\) et \(\lambda = \frac{1}{2}\), alors on appelle aussi la loi, loi de Rayleigh.
Annales où tu peux retrouver la loi de Weibull
Preuve que la loi de Weibull est intéressante à travailler : elle est déjà tombée aux concours. Je te mets ici les liens des sujets :
Ce sujet te permet d’en apprendre plus sur la notion de fiabilité et de risque de défaillance.
Et voilà, c’est tout pour cette fois ! J’espère que cet article t’a plu. Et si tu veux continuer à t’exercer, tu peux retrouver ici toutes nos ressources de mathématiques.












