Salut à toi, jeune préparationnaire ! Voici des fonctions que tu ne vas avoir de cesse de retrouver tout au long de ces deux (ou trois) années. C’est pourquoi il est impératif que non seulement tu te familiarises avec elles et leurs propriétés, mais aussi et surtout que tu les connaisses sur le bout des doigts. Mais ne t’inquiète pas, déroule cet article et tu vas vite te rendre compte qu’en réalité, les fonctions trigonométriques, c’est assez simple.
Tu peux approfondir les notions sur la trigonométrie en consultant notre article sur les fonctions trigonométriques hors programme !
Quel est l’intérêt des fonctions trigonométriques ?
Les fonctions trigonométriques que tu vas voir revenir tout le temps en maths approfondies sont les fonctions : cos, sin, tan et arctan.
Petite information d’ailleurs pour tes colles (puis les oraux) : pense bien à prononcer en entier « cosinus », « arctangente », etc., lors de tes prestations orales en maths. Certains professeurs sont très à cheval là-dessus et ce serait dommage de commencer à les mettre de mauvais poil dès le début de ton exercice.
Ensuite, si les concepteurs raffolent de ces fonctions, c’est qu’outre leurs propriétés propres, elles permettent de construire des exercices très intéressants qui croisent plusieurs notions du programme. Ainsi, un exercice type EDHEC/EM classique revient à étudier les propriétés de la fonction arctan à travers l’étude d’intégrales. Et les polynômes de Tchebychev, dont la définition repose sur celles des fonctions cos et sin, est un grand classique des exercices type Parisiennes.
Leurs domaines de définition
Certaines questions dans les sujets types EDHEC/EM reviennent parfois là-dessus. Pour la rigueur de ta copie, c’est bien sûr important que tu sois bien au point à ce sujet.
- Les fonctions cosinus et sinus sont toutes les deux définies et continues et dérivables sur \(\mathbb{R}\). Elles sont cependant respectivement paire et impaire sur \(\mathbb{R}\).
- La fonction tangente, elle, est continue et dérivable sur \(\mathbb{R} \backslash \{(2k + 1) \frac{\pi}{2}, k \in \mathbb{Z} \} \).
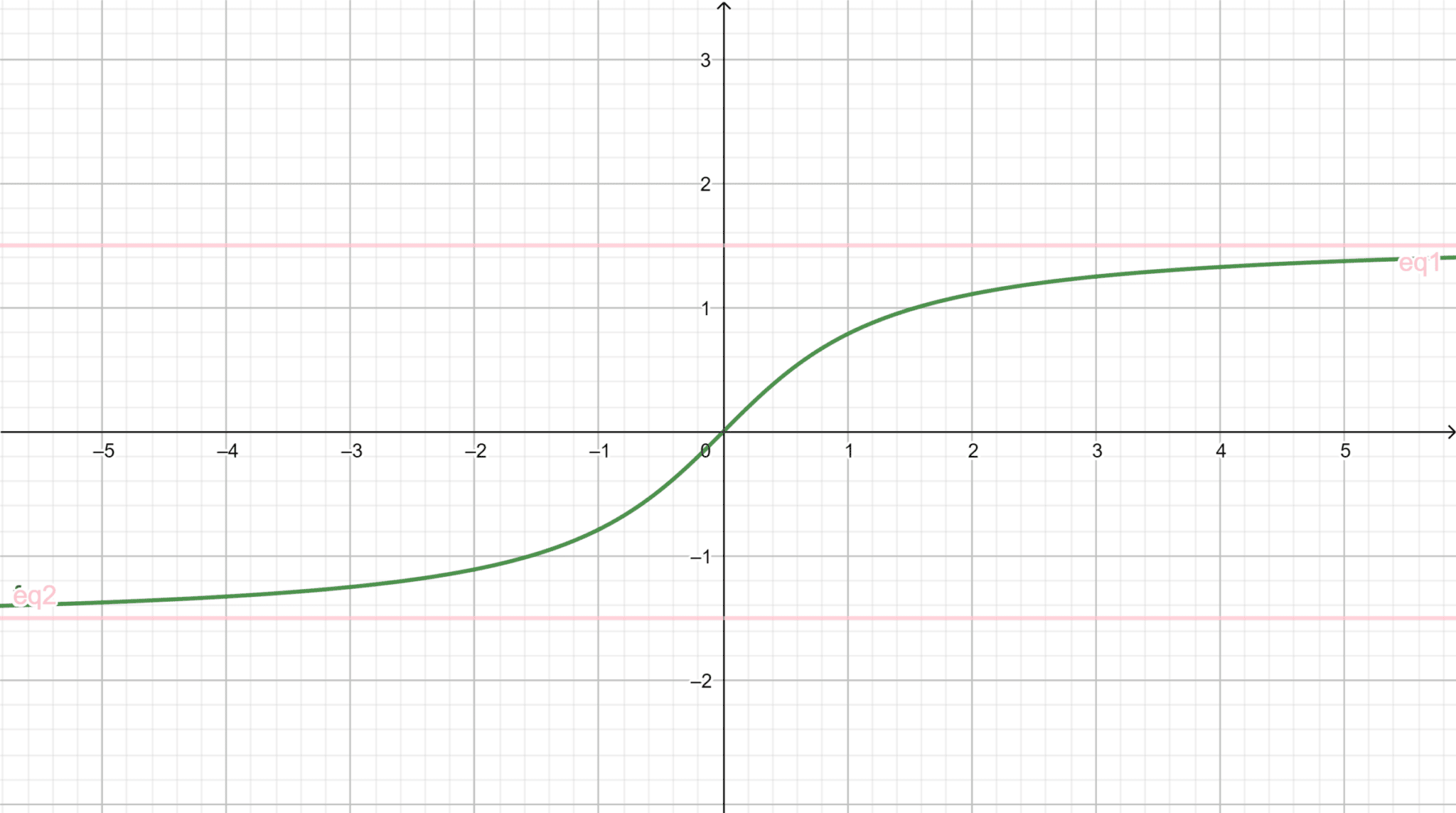
- La fonction arctangente est la bijection réciproque de la fonction tangente, mais restreinte à l’intervalle \([- \frac{\pi} {2}, \frac{\pi} {2}]\). Elle est donc continue sur \(\mathbb{R}\).
La fonction arctangente est représentée ainsi :
Les propriétés des fonctions trigonométriques
Les fonctions trigonométriques possèdent de nombreuses propriétés qui peuvent chacune t’être très utiles. Donc, retiens-les bien !
Sois d’ailleurs précis·e lorsque tu les apprends afin de ne pas oublier par exemple qu’une fonction est strictement croissante, et non seulement croissante, etc. Car les correcteurs sont doublement attentifs à la rigueur lorsqu’il s’agit des fonctions trigonométriques et sans cela, tu peux toi-même facilement t’emmêler les pinceaux.
- Les fonctions cosinus et sinus sont toutes les deux périodiques de période \(2\pi\). Ce qui signifie par exemple que : \(\forall \theta \in \mathbb{R}, \cos(\theta + 2\pi) = \cos(\theta)\).
C’est notamment ce que tu peux observer sur le graphique suivant, qui représente la fonction \(\cos\) en vert et la fonction \(\sin\) en rouge :

- La fonction tangente, elle, est croissante sur \(\mathbb{R} \backslash \{(2k + 1) \frac{\pi}{2}, k \in \mathbb{Z} \} \).
- La fonction arctangente, elle, est strictement croissante sur \(\mathbb{R}\).
- Le sinus établit une bijection de \([- \frac{\pi} {2}, \frac{\pi} {2}]\) sur \([-1, 1]\).
- La cosinus établit une bijection de \([0, \pi]\) sur \([-1, 1]\).
Les formules incontournables
Voici les cinq formules incontournables que tu auras très souvent à utiliser lorsque tu étudieras des fonctions trigonométriques. Tu remarqueras d’ailleurs que les deux dernières peuvent être retrouvées à l’aide des deux premières !
\(\cos(a + b) = \cos(a)\cos(b) – \sin(a)\sin(b)\) \(\sin(a + b) = \sin(a)\cos(b) + \sin(b)\cos(a)\)
\(\cos(a – b) = \cos(a)\cos(b) + \sin(a)\sin(b)\) \(\sin(a – b) = \sin(a)\cos(b) – \cos(a)\sin(b)\)
\(\cos(\theta)^2 + \sin(\theta)^2 = 1\)
Les formules très utiles
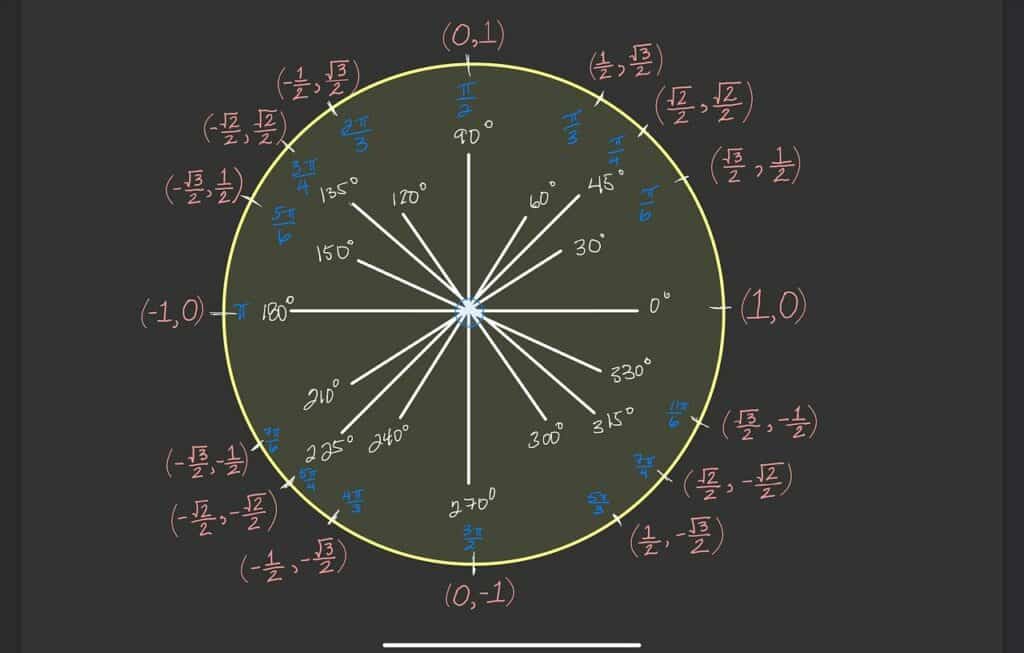
Afin de te faciliter la vie, il existe de nombreuses techniques pour retenir les formules. Celle que je préférais était de tracer rapidement un cercle trigonométrique sur mon papier de brouillon (ou même au tableau lors d’une colle, je l’avais notamment fait aux oraux de l’ESCP et ça leur avait beaucoup plu).
Ensuite, je prenais l’exemple d’un point quelconque sur mon cercle, disons l’angle \(\theta\). Je le reliais avec des lignes droites aux points \(\theta + \pi\) et \(\theta – \pi\), voire éventuellement \(\frac{\pi} {2} – \theta\) et \( \frac{\pi} {2} + \theta \) lorsque cela s’imposait.
Enfin, je n’avais qu’à lire sur ma feuille ou mon tableau les valeurs de \(\sin(\theta + \pi)\) ou \(\cos(\frac{\pi} {2} – \theta)\) par exemple et d’en déduire la formule générale.
À la lecture, ça peut te sembler un peu laborieux, mais je t’assure, entraîne-toi quelques fois et tu verras vite combien c’est simple et rapide. En plus, cela t’évitera de te tromper aux concours sous le coup du stress et de devoir refaire tous tes calculs plus loin.
Mais voici tout de même quelques-unes des formules fondamentales à connaître ou à savoir retrouver
\(\cos(\pi + \theta) = – \cos(\theta)\) \(\cos(\pi – \theta) = \cos(\theta)\) \(\tan(\pi _ \theta) = – \tan(\theta)\)
\(\cos(\frac{\pi} {2} – \theta) = \sin(\theta)\) \(\cos(\frac{\pi} {2} + \theta) = – \sin(\theta)\) \(\tan(\pi + \theta) = \tan(\theta)\)
\(\sin(\pi – \theta) = \sin(\theta)\) \(\sin(\pi + \theta) = – \sin(\theta)\)
\(\sin(\frac{\pi} {2} – \theta) = \cos(\theta\) \(\sin(\frac{\pi} {2} + \theta) = \cos(\theta)\)
Et voilà, te voici maintenant armé·e pour répondre à toutes les questions que l’on pourrait te poser sur les fonctions trigonométriques. À toi de t’entraîner afin de savoir comment exploiter ces outils, bon courage !
Et si tu veux aller plus loin et en savoir plus sur d’autres notions de base, voici quelques articles que je te conseille d’aller lire :
Focus sur les inégalités de convexité
Les suites arithmético-géométriques
Inverser une matrice, c’est facile !