En plus des fonctions trigonométriques classiques qui sont au programme, il en existe quelques autres que tu risques de voir souvent revenir dans les sujets de concours, notamment dans les sujets de type Parisiennes. Voici donc un point sur toutes les fonctions trigonométriques hors programme que tu pourras être amené.e à rencontrer afin d’avoir tous les outils pour savoir les étudier.
Attention, cet article est réservé aux mathématiques approfondies (les fonctions trigonométriques ne sont pas au programme de maths appliquées).
Les fonctions trigonométriques hors programme
Tout comme la fonction \(\arctan\), on étudie parfois les fonctions réciproques de \(cos\) et \(sin\) que sont respectivement les fonctions \(\arccos\) et \(\arcsin\).
De même, bien que ce soit surtout des notions étudiées par les prépas scientifiques, il arrive parfois que les concepteurs des épreuves de maths des prépas commerce s’amusent à utiliser les fonctions des cosinus et sinus hyperboliques. Elles sont définies comme suit :
\(\forall x \in \mathbb{R}, ch(x)=\frac{e^{x}+e^{-x}}{2}\)
\(\forall x \in \mathbb{R}, sh(x)=\frac{e^{x}- e^{-x}}{2}\)
Voici un petit graphique pour t’aider à comprendre (le sinus hyperbolique est représenté en orange et le cosinus hyperbolique en bleu) :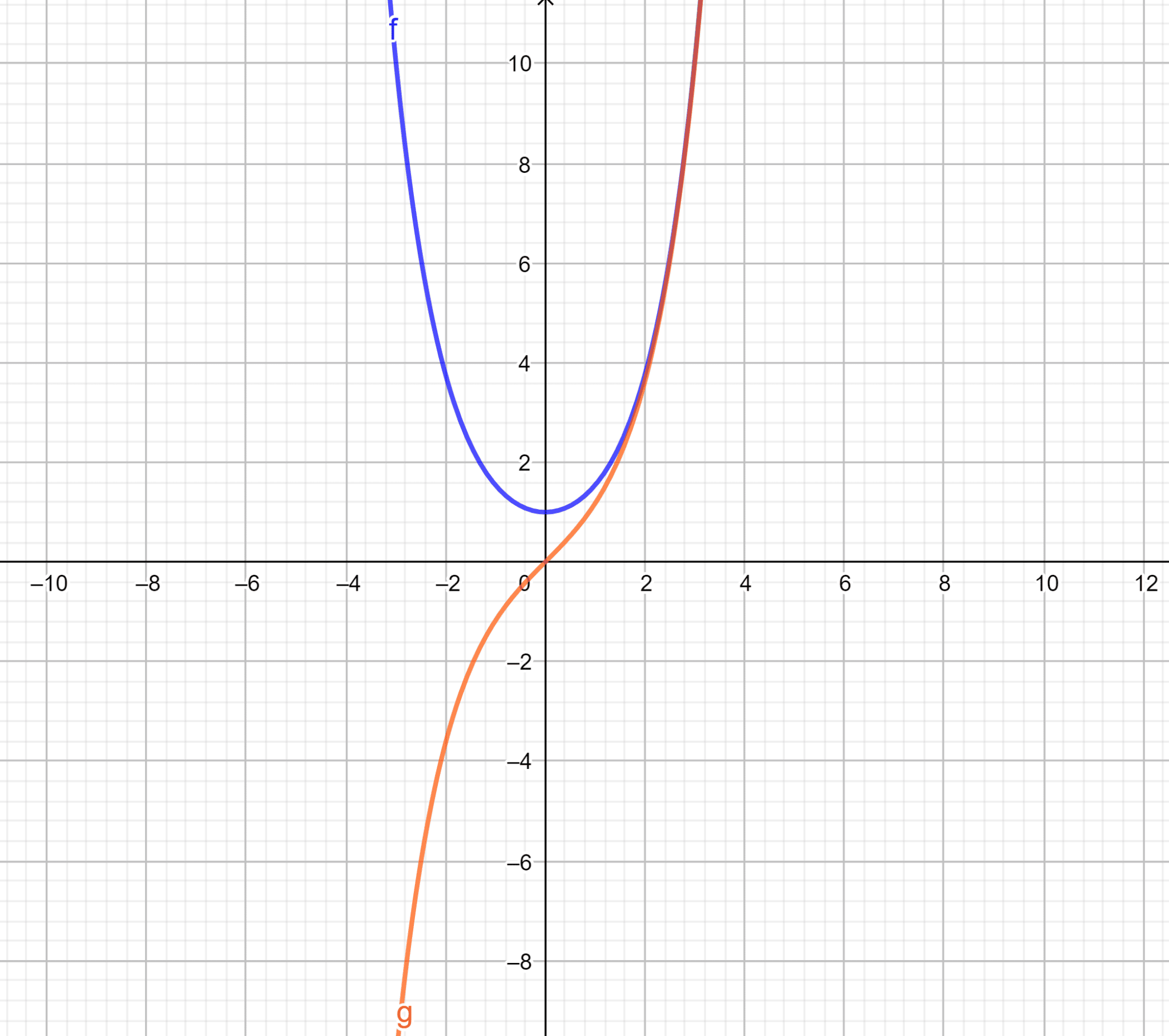
Les domaines de définition des fonctions trigonométriques
En réalité, les fonctions \(\arccos\) et \(\arcsin\) sont les fonctions réciproques de \(cos\) et \(sin\) restreintes à certains intervalles. Ainsi, \(\arccos\) est la fonction réciproque de la fonction \(cos\) restreinte à l’intervalle \([0,\pi]\).
La fonction \(\arcsin\) est, elle, la fonction réciproque de la fonction \(sin\) restreinte à l’intervalle \([- \frac{\pi}{2}, \frac{\pi}{2}]\).
Ainsi, les fonctions \(\arccos\) et \(arcsin\) sont toutes les deux définies et continues sur l’intervalle \([-1,1]\) et à valeurs respectivement dans \([0, \pi]\) et \([- \frac{\pi}{2}, \frac{\pi}{2}]\).
Tu peux t’aider de ce graphique pour mieux les visualiser, \(\arccos\) est représentée en vert et \(\arcsin\) en rouge : 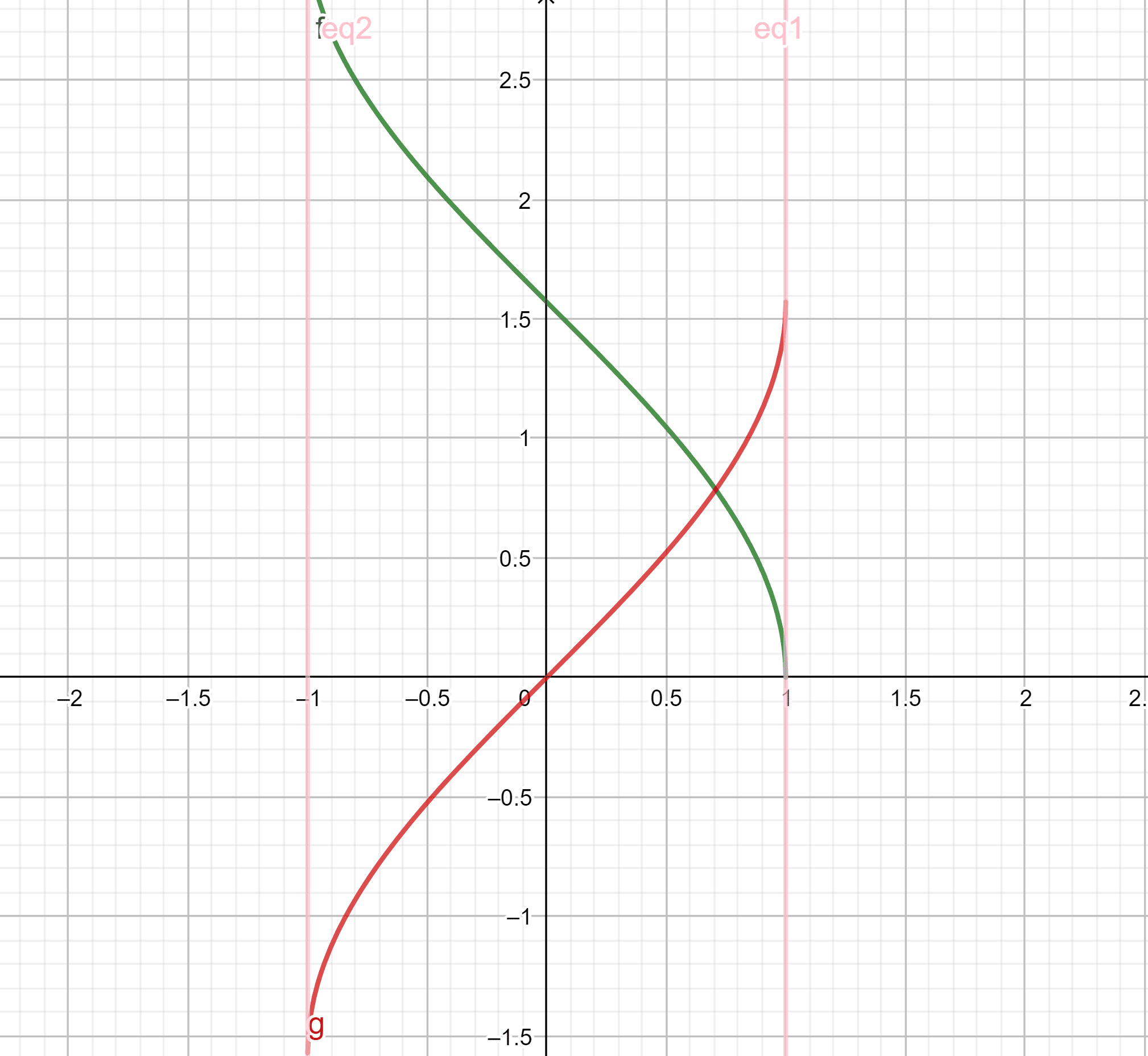
Les deux fonctions hyperboliques sont quant à elles toutes les deux définies sur \(\mathbb{R}\).
Les propriétés à retenir
Tout d’abord, contrairement aux fonctions \(\cos\) et \(\sin\), leurs fonctions réciproques n’admettent pas de parité. Par contre, la fonction \(\arcsin\) est strictement croissante (et continue !) sur \([-1,1]\). Elle définit donc une bijection de \([-1,1]\) sur \([- \frac{\pi}{2}, \frac{\pi}{2}]\).
De leur côté, tout comme les fonctions que tu connais, les fonctions \(ch\) et \(sh\) sont respectivement paire et impaire.
Les formules à connaître
Avant toute chose, un petit rappel sur ce que signifie en mathématiques le fait d’être la fonction réciproque d’une autre fonction.
C’est tout simplement que \(\forall x \in [0, \pi], \arccos(\cos(x)) = x \). Ainsi, de même, on a : \(\forall x \in [- \frac{\pi}{2}, \frac{\pi}{2}], \arcsin(\sin(x)) = x\).
Enfin, si tu veux pouvoir avancer facilement dans un sujet qui fait appel aux fonctions trigonométriques hors programme et avoir des outils pour le comprendre, il est important que tu retiennes ces quelques formules :
- \(\forall x \in [-1,1], \arccos(-x) = \pi – \arccos(x)\)
- \(\sin(\arccos(x)) = \left (\sqrt(1- x^2)\right) \)
- \(\cos(\arcsin(x)) = \left (\sqrt(1- x^2)\right) \)
- \(\forall x\in [-1, 1], \arccos(x) + \arcsin(x) = \frac{\pi}{2} \)
Concernant les \(cosinus\) et \(sinus\) hyperboliques, il existe également de nombreuses formules différentes, mais voici celles que tu dois connaître :
- \(\forall x \in \mathbb{R}, ch(x)^2 – sh(x)^2 = 1\)
\(\forall (a,b) \in \mathbb{R}^{2}\) :
- \(sh(a + b) = sh(a).ch(b) + sh(b).ch(a)\)
- \(ch(a+b) = ch(a).ch(b) + sh(a).sh(b)\)
Tu sais tout sur les fonctions trigonométriques ! À présent, si tu veux aller plus loin et maîtriser d’autres notions hors programme qui reviennent régulièrement, voici quelques faits pour toi :
Les matrices magiques (hors programme ECG)
Matrice compagnon (hors programme ECG)