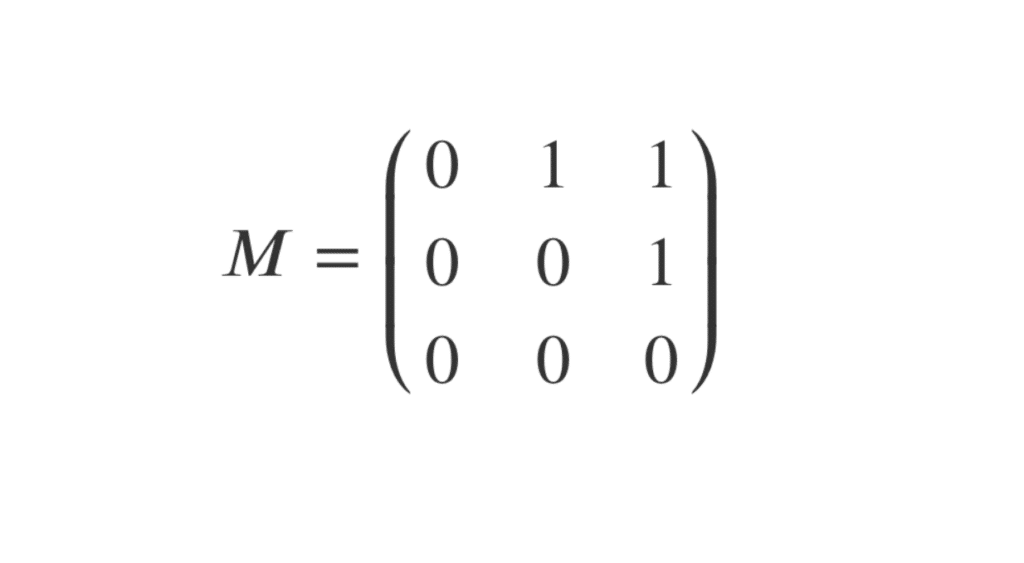Les notions hors programme sont surtout destinées aux candidats se préparant aux épreuves pour accéder aux trois Parisiennes. Cet article met en lumière les notions d’endomorphismes et de matrices nilpotents, se retrouvant assez communément dans les exercices de concours, sans pour autant être au programme.
Pour ne pas que tu sois pris·e au dépourvu quand tu rencontreras ces notions, nous allons donc définir les endomorphismes et les matrices nilpotents. Nous allons t’en présenter les définitions, quelques propriétés ainsi qu’une liste non exhaustive de sujets qui les abordent.
Les notions d’endomorphismes et de matrices nilpotents expliquées en français
Les endomorphismes nilpotents sont particuliers. Si on les compose suffisamment par eux-mêmes, cela donne alors l’endomorphisme nul de l’espace vectoriel associé.
La même définition se retrouve pour les matrices. Une matrice est dite nilpotente si, à partir d’une certaine puissance, le calcul nous donne la matrice nulle dans la dimension de la matrice originale.
Exemple concret d’un endomorphisme et d’une matrice nilpotents
Commençons par un exemple avec une matrice \(M\in\mathcal{M}_{3}(\mathbb{R})\), telle que \(M=\begin{pmatrix} 0 & 1 & 1 \\ 0 & 0 & 1 \\ 0 & 0 & 0\end{pmatrix}\).
Par le calcul, on peut voir que \(M^2=\begin{pmatrix} 0 & 0 & 1 \\ 0 & 0 & 0 \\ 0 & 0 & 0\end{pmatrix}\) et que \(M^3=\begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0\end{pmatrix}\).
Ainsi, \[\forall n \ge 3, M^n=0_{\mathcal{M}_{3}(\mathbb{R})}\]
On dit alors que \(M\) est une matrice nilpotente, d’indice de nilpotence 3.
De la même manière, l’endomorphisme \(f\) de \(\mathbb{R}^{3}\) dans \(\mathbb{R}^{3}\), canoniquement associé à la matrice \(M\), est lui aussi nilpotent. En effet, \[\forall (x,y,z)\in\mathbb{R}^{3}, f(x,y,z)=(y+2z,z,0)\]
Ainsi, \[(f\circ f)(x,y,z)=(z,0,0)\] et donc \[f^3(x,y,z)=(0,0,0)=0_{\mathbb{R}^3}\] et \(f\) est un endomorphisme nilpotent d’indice 3 également, car \[\forall n \ge 3, f^n=0_{\mathbb{R}^3}\]
Définition mathématique d’un endomorphisme et d’une matrice nilpotents
Soit \(E\) un espace vectoriel (de dimension finie ou non) et \(f\) un endomorphisme de \(E\).
\(f\) est un endomorphisme nilpotent d’indice de nilpotence \(n\in\mathbb{N}\) si et seulement si \[\forall i \ge n, f^i=0_E\]
Autrement dit, \(f\) est nilpotent si et seulement s’il existe un polynôme annulateur de la forme \(X^i\), avec \(i\) un entier supérieur ou égal à \(n\), tout en sachant que le polynôme dit minimal (le polynôme annulateur avec le plus petit degré possible) de \(f\) est \(X^n\), \(n\) étant l’indice de nilpotence de l’endomorphisme \(f\).
De la même manière pour les matrices, une matrice \(M\) de l’espace vectoriel \(\mathcal{M}_{dim(F)}(\mathbb{R})\) (\(F\) un espace vectoriel de dimension obligatoirement finie) est dite nilpotente d’indice de nilpotence \(n\) si et seulement si \[\forall i \ge n, M^i=0_F\]
Autrement dit, \(M\) est nilpotente si et seulement s’il existe un polynôme annulateur de la forme \(X^i\), avec \(i\) un entier supérieur ou égal à \(n\), tout en sachant que le polynôme dit minimal de \(M\) est \(X^n\), \(n\) étant l’indice de nilpotence de la matrice \(M\).
Quelques propriétés sur les endomorphismes et les matrices nilpotents
Soit \(E\) un espace vectoriel (de dimension finie), \(f\) un endomorphisme de \(E\) et \(M\) une matrice de \(\mathcal{M}_{dim(E)}(\mathbb{R})\).
Soit \(x\) un vecteur de l’espace vectoriel \(E\), \(p\) est dit indice de \(x\) si \(p\) est le plus petit entier positif tel que \(f^p(x)=0_{E}\).
- Par définition, \(f\) et \(M\) ne possèdent qu’une unique valeur propre égale à 0.
- Ainsi, \(\text {Ker}(f)\ne {0_{E}}\).
- L’indice de nilpotence de l’endomorphisme (respectivement la matrice) est inférieur ou égal à la dimension de l’espace vectoriel de l’endomorphisme (respectivement la matrice).
- Il suffit également que le polynôme caractéristique de \(f\) soit égal à \((-X)^n\), \(n\) étant la dimension de l’espace vectoriel \(E\) (cette propriété fonctionne également pour \(M\)).
- D’après la définition de \(x\), on peut aussi démontrer que la famille \((x,f(x),…,f^{p-1}(x))\) est libre. C’est alors une base du sous-espace qu’elle engendre (que l’on appelle sous-espace cyclique).
- Pour toute matrice \(A\in\mathcal{M}_{dim(E)}(\mathbb{R})\), telle que \(A\) soit strictement triangulaire (c’est-à-dire qu’elle soit triangulaire et de diagonale nulle), alors \(A\) est une matrice nilpotente, car \(A^n=0_{\mathcal{M}_{dim(E)}(\mathbb{R})}\).
- Le déterminant et la trace d’une matrice nilpotente \(M\) sont nuls : toute matrice nilpotente \(M\) n’est donc pas inversible.
- Si \(M\) et \(N\) sont deux matrices carrées qui commutent et qui sont toutes les deux nilpotentes, alors le produit \(MN\) est aussi nilpotent, ainsi que toutes combinaisons linéaires formées avec les deux matrices.
- La notion de nilpotence est tout particulièrement intéressante avec le binôme de Newton. Imaginons une matrice \(A\in\mathcal{M}_{dim(E)}(\mathbb{R})\), telle que \(A=I_{dim(E)}+M\). \(I_{dim(E)}\) et \(M\) commutent et donc, d’après le binôme de Newton appliqué aux matrices, on obtient \[\forall i \ge n, A^i=\displaystyle\sum_{k=0}^{i}{{i}\choose{k}}I^{i-k}_{dim(E)}M^k\] Mais comme \(\forall i \ge n, M^i=0_{\mathcal{M}_{dim(E)}}\), on obtient que \[A^i=\displaystyle\sum_{k=0}^{n}{{i}\choose{k}}I^{i-k}_{dim(E)}M^k\] Souvent, l’indice de nilpotence \(n\) est petit et donc le calcul devient très simple.
- Cette astuce sert également pour les endomorphismes, dont les composées sont alors simplifiées.
Les sujets de concours avec ces notions
Les notions d’endomorphismes et de matrices nilpotents n’ont maintenant plus de secret pour toi. Voici donc une liste d’exercices de concours qui les abordent :