Si tu es en prépa littéraire, notamment en B/L ou en ENS D1 ou D2, voici une fiche portant sur la théorie du consommateur, abordant les notions essentielles ainsi que quelques astuces utiles.
Les définitions essentielles
Variables exogènes : variables ne dépendant pas des décisions de l’agent. Les variables exogènes sont le prix et le revenu. Les consommateurs sont price–takers.
Variables endogènes : variables résultant du choix des consommateurs. Les variables endogènes sont les quantités de biens consommées.
Demande marshallienne : quantité de chaque bien demandée à l’équilibre en fonction du revenu et des prix : xi*(R, p1, p2).
Utilité marginale d’un bien : variation d’utilité lorsque la consommation de ce bien varie, Ceteris paribus (= toutes choses égales par ailleurs). C’est l’utilité retirée de la consommation d’une unité additionnelle d’un bien.
Droite de budget : droite désignant l’ensemble des paniers de biens que le consommateur peut acquérir à revenu et prix fixés.
Courbe d’indifférence : lieu géométrique de l’ensemble des paniers de biens qui procurent au consommateur le même niveau de satisfaction.
L’équilibre du consommateur : point de tangente entre la courbe d’indifférence la plus au nord-est possible et la droite de budget.
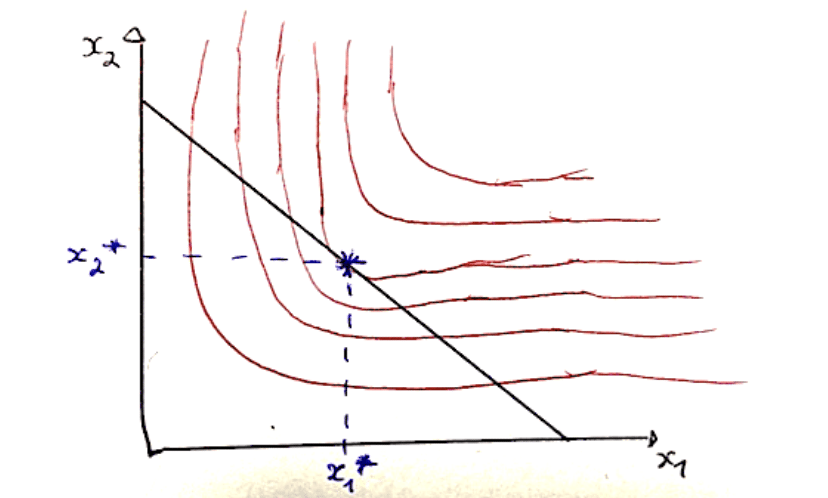
Utilité indirecte : niveau d’utilité maximal atteignable en fonction du revenu du consommateur et des prix.
Solution intérieure : panier comportant des quantités positives pour chacun des biens.
Solution en coin : solution (x*1, x*2) pour laquelle l’un des biens est nul à l’équilibre du consommateur.
Coefficient budgétaire : part du revenu consacré à la consommation d’un bien donné.
Identité de Roy : la demande marshallienne du bien i est égale au rapport entre la désutilité marginale liée à la hausse du prix du bien i et l’utilité marginale du revenu. Ci-dessous, la fonction d’utilité indirecte est notée V.
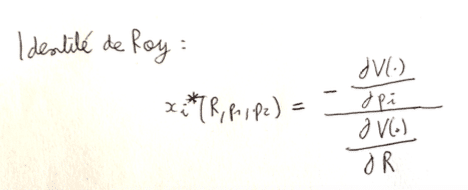
Courbe consommation-revenu ou sentier d’expansion du revenu : lieu géométrique des différents équilibres du consommateur lorsque le revenu varie, à prix constants.
Courbe d’Engel : lieu géométrique des points qui associent, à chaque niveau de revenu, la quantité consommée d’un bien à l’équilibre, pour un couple de prix fixe.
Le cadre d’analyse de la théorie des choix du consommateur
La plupart du temps, on raisonne dans une économie avec deux biens, notés 1 et 2. Les préférences du consommateur sont représentées par la fonction d’utilité U (x1, x2). Cette fonction est croissante et concave : l’utilité marginale est décroissante, d’après la première loi de Gossen, et positive, d’après l’axiome de non-satiété.
Le programme du consommateur va être de maximiser son utilité sous la contrainte de son budget. Il va devoir choisir les quantités de biens 1 et de biens 2 qui répondent à ses conditions.
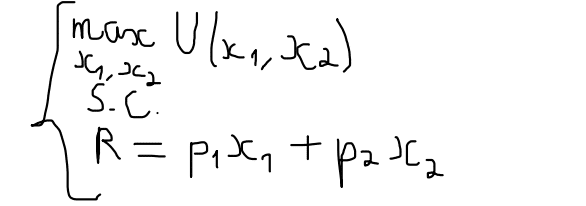
Quelques astuces importantes
- Dans le cas d’une fonction d’utilité de type Cobb-Douglas, les courbes d’Engel sont toujours linéaires croissantes et passent par l’origine du repère.
- Pour trouver les équations des courbes consommation-revenu et consommation-prix, il faut partir de l’égalité TMS = p1/p2.
- L’équation de la courbe de demande individuelle pour le bien i (dans le plan (pi,xi)) est donnée par x*i (R, pi, pj), c’est-à-dire la demande marshallienne du bien i pour le revenu et le prix du bien j fixés. Avec le prix en abscisse et la quantité en ordonnée.
- Pour trouver les équations des courbes d’Engel, il faut partir des demandes marshalliennes et poser une fonction f(R), où R est le revenu.
- Lorsqu’on a une fonction d’utilité, il faut toujours se demander s’il est possible d’avoir des solutions en coin. Une solution en coin existe lorsque l’utilité est non nulle, alors même que la quantité d’un des biens est nulle. Le raisonnement graphique peut aider à s’en apercevoir.
- Quand les quantités à l’équilibre x*1 et x*2 de la solution intérieure sont négatives simultanément, il faut comparer les utilités des solutions en coin et choisir celle possédant l’utilité la plus grande.
- Pour tracer une courbe d’Engel ou une courbe de consommation-revenu lorsqu’on ne connaît pas la valeur des prix des biens, il faut les considérer comme des constantes et tracer les courbes avec des formes générales.
- Si on observe que la courbe d’indifférence sera asymptotique, il faut les limites de la fonction d’indifférence en 0 et en + l’infini. Si la courbe admet des solutions en coin, il faut calculer f(0) et f(x1)= 0.
- Dans la solution intérieure, lorsque la quantité d’un bien est négative pour une certaine valeur du revenu, on préférera à la place la solution en coin, pour laquelle la quantité du bien en question est égale à 0.













