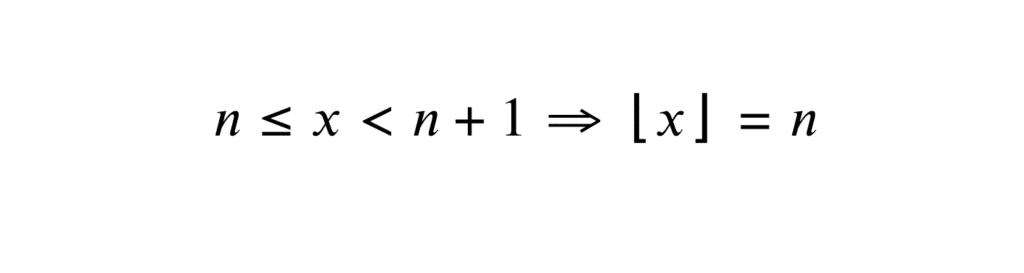La fonction partie entière, souvent notée \(\lfloor x \rfloor\), est un concept mathématique fondamental en analyse, notamment utilisée dans des contextes variés en analyse, en probabilités, et en informatique. Cette fonction associe à tout nombre réel \(x\) le plus grand entier inférieur ou égal à \(x\). Comprendre et manipuler cette fonction est crucial pour les étudiants en classes préparatoires ECG, car elle intervient dans de nombreux problèmes d’optimisation, d’analyse et de probabilités. Cet article propose plusieurs astuces essentielles pour maîtriser l’utilisation de la fonction partie entière.
1. Expression de la partie entière avec des inégalités
\[
n \leq x < n+1 \Rightarrow \lfloor x \rfloor = n
\]
Cette relation est la définition même de la fonction partie entière. Elle est utile pour encadrer \(x\) entre deux entiers consécutifs. Cela permet de résoudre des problèmes où l’on doit évaluer la position d’un réel par rapport à ses voisins entiers.
2. Relation entre la partie entière d’un réel et de son opposé
\[
\lfloor x \rfloor + \lfloor -x \rfloor =
\begin{cases}
0 & \text{si } x \text{ est entier} \\
-1 & \text{sinon}
\end{cases}
\]
Cette astuce montre comment la partie entière de \(x\) et celle de son opposé \(-x\) sont liées. Cela est particulièrement utile dans les problèmes impliquant des symétries ou des conditions périodiques.
3. Calcul d’une probabilité avec un partie entière pour une variable aléatoire à densité
Pour calculer la probabilité que la partie entière \(\lfloor X \rfloor\) d’une variable aléatoire \(X\) à densité soit égale à un entier \(k\), on peut exprimer cela en termes de la probabilité que \(X\) soit inférieur à \(k+1\) mais pas moins que \(k\). Cela se traduit par la différence des probabilités cumulées aux points \(k+1\) et \(k\) :
\[
P(\lfloor X \rfloor = k) = P(X < k+1) – P(X < k)
\]
Cette formule est dérivée directement du calcul des probabilités pour des intervalles continus, transformant l’évaluation en un calcul simple entre deux valeurs cumulatives de la distribution de \(X\). Cette approche est extrêmement utile pour analyser la distribution de la partie entière d’une variable continue, permettant de clarifier le passage du continu au discret dans les modèles économiques et statistiques.
4. Unicité de la partie entière
L’unicité de la partie entière est une de ses propriétés les plus importantes et tu pourrais être amené à la démontrer aux oraux de mathématiques. Nous pouvons la démontrer comme cela : soit la partie entière, \(\lfloor x \rfloor,\) d’un nombre réel \(x\), supposons pour l’absurde que deux entiers \(n\) et \(m\) (avec \(n \neq m\)) satisfont la définition de la partie entière pour \(x\), c’est-à-dire :
\[
n \leq x < n+1 \quad \text{et} \quad m \leq x < m+1
\]
On suppose sans perte de généralité que \(n < m\). Alors, par transitivité, on a :
\[
n < m \leq x < n+1
\]
Ce qui implique que \(m – n < 1\). Or, \(m\) et \(n\) étant des entiers distincts, \(m-n\) est un entier positif, donc \(m-n \geq 1\). Ceci contredit l’inégalité \(m – n < 1\), démontrant ainsi que l’hypothèse \(n \neq m\) est fausse. Par conséquent, il ne peut y avoir qu’un seul entier \(n\) tel que :
\[
n \leq x < n+1
\]
Ceci prouve l’unicité de la partie entière \(\lfloor x \rfloor\) de \(x.\)
5. Décomposition d’un réel en partie entière et fractionnaire
\[
x = \lfloor x \rfloor + \{x\}
\]
où \(\{x\}\) représente la partie fractionnaire de \(x\), c’est-à-dire \(x – \lfloor x \rfloor\). Cette décomposition est cruciale pour analyser des fonctions qui manipulent séparément les composantes entière et fractionnaire d’un nombre. Cela peut aussi simplifier des calculs de sommes et également te permettre des résoudre des équations et des inéquations avec des parties entières.
6. Calcul de la somme des parties entières d’une séquence arithmétique
Une astuce plus orientée vers les calculs pratiques avec la fonction partie entière concerne la somme des parties entières pour une séquence arithmétique. Supposons que nous voulions calculer la somme \( \displaystyle \sum_{k=1}^n \lfloor ak + b \rfloor \), où \(a\) et \(b\) sont des constantes. Cette tâche peut sembler complexe, mais elle peut être simplifiée par une analyse segmentée basée sur les valeurs que prend \(\lfloor ak + b \rfloor\) en fonction de \(k\).
Pour ce faire, divisons la somme en segments où \( \lfloor ak + b \rfloor \) change de valeur, ce qui se produit chaque fois que \(ak + b\) passe par un entier. Les points où cela se produit sont les valeurs de \(k\) telles que \(ak+b\) est un entier, c’est-à-dire \(k = \frac{m-b}{a}\) pour \(m\) entier. Cela signifie que la fonction partie entière change de valeur à des points spécifiques qui peuvent être calculés à l’avance.
Une fois que vous avez identifié ces points, la somme peut être scindée en intervalles où \( \lfloor ak + b \rfloor \) est constante. La somme sur chaque intervalle peut être calculée en multipliant la valeur constante de \( \lfloor ak + b \rfloor \) par le nombre de termes dans cet intervalle, simplifiant grandement le calcul initial.
7. Utilisation de la fonction partie entière pour résoudre des inéquations
La fonction partie entière peut être exploitée pour résoudre des inéquations impliquant des expressions complexes. Par exemple, considérons l’inéquation \(\lfloor x \rfloor + 2x > 5\). Pour résoudre cette inéquation, on doit d’abord identifier pour quels \(x\), \(\lfloor x \rfloor + 2x\) dépasse 5. Une méthode consiste à séparer les cas en fonction des valeurs entières que peut prendre \(\lfloor x \rfloor\), et ensuite analyser l’inéquation pour chaque intervalle:
\[
\lfloor x \rfloor = n \Rightarrow n + 2x > 5 \Rightarrow x > \frac{5 – n}{2}
\]
En évaluant cette inéquation pour différentes valeurs de \(n\), on obtient des intervalles spécifiques de \(x\) pour lesquels l’inéquation est satisfaite.
8. Calcul de l’intégrale de la fonction partie entière sur un intervalle
Pour calculer l’intégrale de la fonction partie entière \(\lfloor x \rfloor\) sur un intervalle \([a, b]\) où \(a\) et \(b\) sont des entiers, on peut transformer cette intégrale en une somme de valeurs constantes prises par \(\lfloor x \rfloor\) sur des sous-intervalles entiers. Voici la démarche :
1. Segmentation de l’intervalle : L’intégrale de \(\lfloor x \rfloor\) de \(a\) à \(b\) peut être segmentée en intégrales sur les intervalles \([k, k+1[\) pour \(k\) allant de \(a\) à \(b-1\).
2. Expression de l’intégrale : Sur chaque intervalle \([k, k+1[\), \(\lfloor x \rfloor = k\). Ainsi, l’intégrale sur cet intervalle est simplement :
\[
\int_k^{k+1} \lfloor x \rfloor \, dx = \int_k^{k+1} k \, dx = k \times (k+1 – k) = k
\]
3. Somme des intégrales : L’intégrale totale est alors la somme de toutes ces intégrales élémentaires sur chaque intervalle :
\[
\int_a^b \lfloor x \rfloor \, dx = \sum_{k=a}^{b-1} k
\]
4. Calcul de la somme : La somme \( \displaystyle \sum_{k=a}^{b-1} k\) est une somme arithmétique qui peut être exprimée et calculée directement :
\[
\sum_{k=a}^{b-1} k = \frac{(b-1 – a + 1)(a + (b-1))}{2} = \frac{(b-a)(a+b-1)}{2}
\]
En utilisant cette méthode, l’intégrale de la fonction partie entière sur l’intervalle \([a, b]\) est calculée efficacement par transformation en une somme arithmétique simple. Cette approche démontre une connexion profonde entre l’analyse intégrale et la sommation discrète pour les fonctions à valeurs entières.
9. Utilisation dans les sommes et les séries
\[
\sum_{k=1}^n \lfloor x+k \rfloor = nx + \frac{n(n-1)}{2} – \sum_{k=1}^n \{x+k\}
\]
Cette formule illustre l’intégration de la fonction partie entière dans le calcul de sommes. Cette nouvelle forme ci-dessus utilise la partie fractionnaire des réels étudiés, cette nouvelle expression peut être très utile notamment après une simple minoration de la dernière somme. En effet le terme général de la dernière somme peut être majoré par 1 et cette somme peut donc être majorée par \(n.\) Finalement la première somme peut être minorée par \( n(x-1) + \displaystyle \frac{n(n-1)}{2}.\)
Conclusion
La maîtrise de la fonction partie entière ouvre la voie à une multitude d’applications en mathématiques, notamment dans l’étude des fonctions discontinues et des modèles de planification et d’optimisation. Les astuces présentées ici permettent une meilleure intégration des propriétés et des particularités de cette fonction dans ton arsenal mathématique. À travers ces techniques, tu pourras aborder des problèmes avec plus d’efficacité et de précision.
Pour t’entrainer à manipuler la partie entière tu peux réaliser les sujets mathématiques approfondies suivants :
Tu peux retrouver ici toutes autres ressources mathématiques !