Dans cet article, tu trouveras les démonstrations des formules de trigonométrie qu’il faudra connaître pour les concours. En effet, cela pourrait être utile pour éviter de toutes les apprendre par cœur (et donc de perdre du temps, sans oublier le risque de te tromper), car elles se retrouvent facilement, en n’en connaissant que cinq !
Attention, cet article est réservé aux maths approfondies, la trigonométrie n’étant pas au programme des maths appliquées.
Petits rappels de trigonométrie
Pour en savoir plus sur les fonctions trigonométriques, je t’invite à consulter cet article.
Dans tout l’article, on prend \(a\) et \(b\) deux réels.
Les valeurs à connaître
Voici un tableau récapitulatif à connaître par cœur :
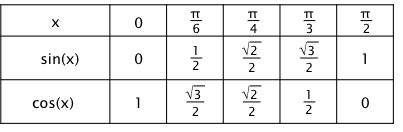
Les formules à connaître
Ces cinq formules classiques sont à connaître par cœur. Elles vont te servir pour retrouver celles que je vais démontrer juste en dessous.
- \(\cos^{2}(a)+\sin^{2}(a)=1\)
- \(\cos(a+b)=\cos(a)\cos(b)-\sin(a)\sin(b)\)
- \(\cos(a-b)=\cos(a)\cos(b)+\sin(a)\sin(b)\)
- \(\sin(a+b)=\cos(a)\sin(b)+\cos(b)\sin(a)\)
- \(\sin(a-b)=\cos(a)\sin(b)-\cos(b)\sin(a)\)
Démonstration des autres formules
cos(2a) et sin(2a)
- Montrons que \(\cos(2a)=2\cos^{2}(a)-1=1-2\sin^{2}(a)\)
\(
\begin{align}
\cos(2a)&=\cos(a+a)\\
&=\cos(a)\cos(a)-\sin(a)\sin(a)\\
&=\cos^{2}(a)-\sin^{2}(a)\\
&=cos^{2}(a)-(1-\cos^{2}(a))\\
&=2\cos^{2}(a)-1
\end{align}
\)
D’où \[ \fbox{\( \displaystyle \cos(2a)=2\cos^{2}(a)-1\)}\]
De la même manière :
\(
\begin{align}
\cos(2a)&=\cos(a+a)\\
&=\cos(a)\cos(a)-\sin(a)\sin(a)\\
&=\cos^{2}(a)-\sin^{2}(a)\\
&=(1-\sin^{2}(a))-\sin^{2}(a)
&=1-2\sin^{2}(a)
\end{align}
\)
D’où \[ \fbox{\( \displaystyle \cos(2a)=1-2\sin^{2}(a)\)}\]
- Montrons que \(\sin(2a)=2\sin(a)\cos(a)\)
\(
\begin{align}
\sin(2a)&=\sin(a+a)\\
&=\sin(a)\cos(a)+\cos(a)\sin(a)\\
&=2\sin(a)\cos(a)
\end{align}
\)
D’où \[ \fbox{\( \displaystyle \sin(2a)=2\sin(a)\cos(a)\)}\]
Transformation de produits en sommes
Ces formules peuvent être très utiles, notamment lorsqu’il faut calculer une intégrale.
- Montrons que \(\displaystyle \cos(a)\cos(b)=\frac{1}{2}(\cos(a-b)+cos(a+b))\)
D’après le cours, \(\cos(a+b)=\cos(a)\cos(b)-\sin(a)\sin(b)\) et \(\cos(a-b)=\cos(a)\cos(b)+\sin(a)\sin(b)\).
En additionnant ces deux égalités, on a :
\(2\cos(a)\cos(b)=\cos(a+b)+\cos(a-b)\)
D’où \[ \fbox{\( \displaystyle \cos(a)\cos(b)=\frac{1}{2}(\cos(a+b)+\cos(a-b)\)}\]
- Montrons que \(\displaystyle \sin(a)\sin(b)=\frac{1}{2}(\cos(a-b)-\cos(a+b))\)
D’après le cours, \(\displaystyle \cos(a+b)=\cos(a)\cos(b)-\sin(a)\sin(b)\) et \(\cos(a-b)=\cos(a)\cos(b)+\sin(a)\sin(b)\).
En soustrayant :
\(
\begin{align}
\cos(a-b)-\cos(a+b)&=(\cos(a)\cos(b)+\sin(a)\sin(b))-(\cos(a)\cos(b)-\sin(a)\sin(b))\\
&=2\sin(a)\sin(b)
\end{align}
\)
D’où \[ \fbox{\( \displaystyle \sin(a)\sin(b)=\frac{1}{2}(\cos(a-b)-\cos(a+b)\)}\]
- Montrons que \(\displaystyle \sin(a)\cos(b)=\frac{1}{2}(\sin(a-b)+\sin(a+b))\)
D’après le cours, \(\displaystyle \sin(a+b)=\cos(a)\sin(b)+\cos(b)\sin(a)\) et \(\sin(a-b)=\cos(a)\sin(b)-\cos(b)\sin(a)\).
En additionnant ces deux égalités, on a :
\(2\sin(a)cos(b)=\sin(a+b)+\sin(a-b)\)
D’où \[ \fbox{\( \displaystyle \sin(a)\cos(b)=\frac{1}{2}(\sin(a-b)+\sin(a+b)\)}\]
Formules de linéarisation
- Montrons que \(\displaystyle \cos^{2}(a)=\frac{1}{2}(1+\cos(2a))\)
D’après la démonstration précédente, \(\displaystyle \cos(a)\cos(b)=\frac{1}{2}(\cos(a-b)+cos(a+b))\).
D’où :
\(\displaystyle \cos(a)\cos(a)=\frac{1}{2}(\cos(a-a)+cos(a+a))\)
\(\Leftrightarrow\)
\(\cos^{2}(a)=\frac{1}{2}(\cos(0)+\cos(2a))\)
D’où, finalement, \[ \fbox{\( \displaystyle \cos^{2}(a)=\frac{1}{2}(1+\cos(2a))\)}\]
- De la même manière, on montre que
\[ \fbox{\( \displaystyle \sin^{2}(a)=\frac{1}{2}(1-\cos(2a))\)}\]
Transformation de sommes en produits
Dans un exercice, comme dans HEC 2018, les formules suivantes seront données, et tu devras les démontrer. On part alors d’un côté de l’équation pour prouver l’égalité.
- Montrons que \(\displaystyle \cos(a)+\cos(b)=2\cos(\frac{a+b}{2})\cos(\frac{a-b}{2})\)
On sait que \(\displaystyle \cos(a)\cos(b)=\frac{1}{2}(\cos(a-b)+cos(a+b))\)
En remplaçant \(a\) par \(\displaystyle \frac{a+b}{2}\) et \(b\) par \(\displaystyle \frac{a-b}{2}\) dans l’égalité précédente, on a :
\(\displaystyle \cos(\frac{a+b}{2})\cos(\frac{a-b}{2})=\frac{\cos(\frac{a+b}{2}+\frac{a-b}{2})+\cos(\frac{a+b}{2}-\frac{a-b}{2})}{2}\)
En simplifiant, on obtient :
\(\displaystyle \cos(\frac{a+b}{2})+\cos(\frac{a-b}{2})=\frac{\cos(a)+\cos(b)}{2}\)
D’où, finalement : \[ \fbox{\( \displaystyle 2\cos(\frac{a+b}{2})+\cos(\frac{a-b}{2})=\cos(a)+\cos(b) \)}\]
- Montrons que \(\displaystyle \cos(a)-\cos(b)=-2\sin(\frac{a+b}{2})\sin(\frac{a-b}{2})\)
On sait que \(\displaystyle \sin(a)\sin(b)=\frac{1}{2}(\cos(a-b)-\cos(a+b))\)
En remplaçant \(a\) par \(\displaystyle \frac{a+b}{2}\) et \(b\) par \(\frac{a-b}{2}\) dans l’égalité précédente, on a :
\(\displaystyle \sin(\frac{a+b}{2})\sin(\frac{a-b}{2})=\frac{\cos(\frac{a+b}{2}-\frac{a-b}{2})-\cos(\frac{a+b}{2}+\frac{a-b}{2})}{2}\)
En simplifiant, on obtient :
\(\displaystyle \sin(\frac{a+b}{2})\sin(\frac{a-b}{2})=\frac{\cos(b)-\cos(a)}{2}\)
D’où \[ \fbox{\( \displaystyle \cos(a)-\cos(b)=-2\sin(\frac{a+b}{2})\sin(\frac{a-b}{2})\)}\]
- Montrons que \(\displaystyle \sin(a)+\sin(b)=2\sin(\frac{a+b}{2})\cos(\frac{a-b}{2})\)
On sait que \(\displaystyle \sin(a)\cos(b)=\frac{1}{2}(\sin(a-b)+\sin(a+b))\)
De la même manière que les démonstrations précédentes, on remplace \(a\) par \(\displaystyle \frac{a+b}{2}\) et \(b\) par \(\frac{a-b}{2}\) dans l’égalité et on obtient :
\[ \fbox{\( \displaystyle\sin(a)+\sin(b)=2\sin(\frac{a+b}{2})\cos(\frac{a-b}{2})\)}\]
- Montrons que \(\displaystyle \sin(a)-\sin(b)=2\cos(\frac{a+b}{2})\sin(\frac{a-b}{2})\)
De la même façon que dans les démonstrations précédentes, on trouve
\[ \fbox{\( \displaystyle\sin(a)-\sin(b)=2\cos(\frac{a+b}{2})\sin(\frac{a-b}{2})\)}\]
J’espère que cet article t’aura plu, te voici maintenant pro en trigo ! N’hésite pas à consulter toutes nos ressources en mathématiques.











